Hey people, having some difficulty with the y^2=f(x) graphs, i get how to find the domain and the turnings points, though i stumble upon the shape of the curve:/
Can someone like give me steps in finding the correct shape of the curves, just in general?
Example 1
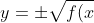})
Let's have some function.
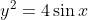
We can begin by consider that this is just the equivalent of
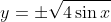
. There are a few things we need to consider.
Consider the case of
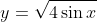
first.
Let's draw the sine function first with an amplitude of 4. It should look something like this.

This is the graph of

Now what we want to do since it is periodic, meaning the same at certain intervals, we just want to consider one lump per cycle.

We know that we cannot square root a negative number for graphing, so the negative portion is ignored for now. Your graph shall look like this now:

Now we can finally begin. Let's first consider the line
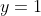
(This is because when we square root 1 we get 1 so the new function stays at the same oordinate of 1!) It will divide the region into two regions. I have named the top region, region 1 and the lower region, region 2.

I will start with the top, since it's the top dog!

Some noticeable points of course is the stationary points (maximum turning points!) It is a 4. When we are taking the square root, there is still a stationary point at the x value, but not necessarily at that y value. So the y value will be square rooted. It will be at 2 now.

Staying at region 1, we know that for what ever values greater than 1, if it is square rooted, it will be less than their original y coordinate, so here we go. Your graph should look like this now.

Finally, region 2 will be considered. We notice that all the y coordinates are one and below for this region but greater or equal to zero.
When we square root zero, we get of course zero. So look in those points! They remain the same. So if we have a y coordinate of zero. It will be there once we square root the function.

Now in between 0 and 1, something interesting happens.
All y coordinates are give by 0<y<1.
So we have something like 0.25. If we square root that. we actually get a larger value. Eg. 0.5, So the corresponding y coordinate of the square rooted function will be larger than the original function!

Walhaaaa... We got the function
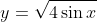
We also wanted
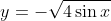
No worries, simply reflect it about the x axis. Like so.
 Example 2
Example 2
Normally we are not fortunate, the function is note stated. We are normally given a graph like this and asked to sketch:
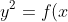)

Let's apply the method I have shown you above.
First draw the line
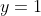
If I did not explain before, I drew this line because we are actually considering the y values of 1. So whenever the graph intersects at y=1, and we square root this graph, we are in the exact same position.
Similarly, if we square root the oordinates of:
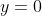
(x intercepts.) It would equal 0 and remain in the exact same position!

Here, we need to estimate where
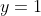
is.

Somewhere there will be appropriate. Not exact. But pretty. Anyway,
The two regions will be called Region Zee and Region Bob.
As we have said, mark out when y=1, and y=0,

Like so.
So Region Zee, we notice that our maximum value is 4. When we square root 4 as the y oordinate, it will bring it back to 2.

And I have also said, for values greater than 1, no matter what y coordinate you square root, it will always drag it down into a smaller value. That being in mind we are now at this stage:

Time for region BOB.

As we have discussed the concept before, what ever y coordinates for 0<y<1 (Eg. 0.64) is square rooted, we always get a larger value. (0.8).
So the square rooting the old function will bring the new function up. And here we have the function of
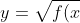})

Last of all, we know that
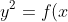)
was made up of two functions if you like.
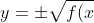})
. We have already drawn the positive case, to get the negative case simply reflect about x axis.
Now, never forget to label your points that were given onto your new function even though they are transformed!
IT'S A FISHY! RAWWWRR!

I will stop there and continue upon request as I am exhausted.
Summarising to graph
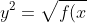})
- Mark where
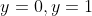
- Consider the region
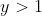
- Consider the region
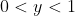
- Reflect according to the x axis.
- Mark out any known points before and after reflection.














