HSC 2012 MX1 Marathon #1 (archive) (3 Viewers)

[AAEldar]

Re: 2012 HSC MX1 Marathon

wouldnt it be sqroot(16-t^2)/4

Yes, yes it would :\

 

[kingkong123]

Re: 2012 HSC MX1 Marathon

15

the answer is 19. i got it by expanding and it didn't take as long as i expected, but is there a way of doing it without expansion? using binomial theorem or something?

 

[Octagon]

Re: 2012 HSC MX1 Marathon

Trig Help
A vertical tower of height h meters stands at the top of a slope of inclination A to the horizontal. An observer at the foot of the slope finds the angle of elevation of the top of the tower to be B. The observer walks a distance d m up a line of greatest slope, towards the foot of the tower, and finds the angle of elevation of the top of the tower to be Y. If the observer is then x m away from the foot of the tower, prove that
a. h=dsin(B-A)sin(Y-A)/sin(Y-B)cosA
b. x=dsin(B-A)cosY/sin(Y-B)cosA

 

[bleakarcher]

Re: 2012 HSC MX1 Marathon

the answer is 19. i got it by expanding and it didn't take as long as i expected, but is there a way of doing it without expansion? using binomial theorem or something?

Yeh, sorry made a mistake yesterday. You dont have to expand to whole thing you only have to expand part of it then analyse to find the constant term.
(x+1+x^(-1))^4=(x+1+x^(-1))^2(x+1+x^(-1))^2=[(x+1)^2+2x^(-1)(x+1)+x^(-2)](x+1+x^(-1))^2=[x^2+2x+2x^(-1)+x^(-2)+3][x^2+2x+2x^(-1)+x^(-2)+3]
Hence, constant term=1*1+2*2+2*2+1*1+3*3=19

 

[nightweaver066]

Re: 2012 HSC MX1 Marathon

Use the method of bisection to solve to 2 decimal places:

 

[cutemouse]

Re: 2012 HSC MX1 Marathon

Yeh, sorry made a mistake yesterday. You dont have to expand to whole thing you only have to expand part of it then analyse to find the constant term.
(x+1+x^(-1))^4=(x+1+x^(-1))^2(x+1+x^(-1))^2=[(x+1)^2+2x^(-1)(x+1)+x^(-2)](x+1+x^(-1))^2=[x^2+2x+2x^(-1)+x^(-2)+3][x^2+2x+2x^(-1)+x^(-2)+3]
Hence, constant term=1*1+2*2+2*2+1*1+3*3=19

I think you might be able to complete the square on x+x^(-1), but I haven't tried that yet...

 

[deswa1]

Re: 2012 HSC MX1 Marathon

This is an interesting question:

Consider a circle with equation <a href="http://www.codecogs.com/eqnedit.php?latex=x^2@plus;y^2=10" target="_blank"><img src="http://latex.codecogs.com/gif.latex?x^2+y^2=10" title="x^2+y^2=10" /></a>. From the point P (-3,4), two tangents to the circle are drawn. Find the angle between these two tangents.

 

[Drongoski]

Re: 2012 HSC MX1 Marathon

This is an interesting question:

Consider a circle with equation <a href="http://www.codecogs.com/eqnedit.php?latex=x^2@plus;y^2=10" target="_blank"><img src="http://latex.codecogs.com/gif.latex?x^2+y^2=10" title="x^2+y^2=10" /></a>. From the point P (-3,4), two tangents to the circle are drawn. Find the angle between these two tangents.

Is answer ?:

 

[deswa1]

Re: 2012 HSC MX1 Marathon

Is answer ?:

Yep. That's what me and a few friends got but we don't have the actual answer so I can't tell you 100%. I'm pretty confident though. How did you get it so fast, my method was quite complicated... If you don't want to type it all out, can you just post a general outline of your working

 

[Carrotsticks]

Re: 2012 HSC MX1 Marathon

How did you get it so fast

Because Drongoski is brilliant.

 

[Drongoski]

Re: 2012 HSC MX1 Marathon

I got the answer in 1 minute. Unfortunately I'm hopeless in putting up a diagram. But I'll explain.

Circle is centered at origin with radius sqrt(10) and the external point (-3,4) has distance of 5 from the centre.{3,4,5} is a Pythagorean triple - so the 5 is immediate. Drawing the 2 tangents to the circle: consider 1 of the 2 congruent right-angled triangles: hypotenuse 5 and one of the shorter sides = sqrt(10). By Pythag Thm, remaining side is sqrt(15). Therefore half the required angle has tan = sqrt(10)/sqrt(15). Hence answer.

 

[SpiralFlex]

Re: 2012 HSC MX1 Marathon

I got the answer in 1 minute. Unfortunately I'm hopeless in putting up a diagram. But I'll explain.

Circle is centered at origin with radius sqrt(10) and the external point (-3,4) has distance of 5 from the centre.{3,4,5} is a Pythagorean triple - so the 5 is immediate. Drawing the 2 tangents to the circle: consider 1 of the 2 congruent right-angled triangles: hypotenuse 5 and one of the shorter sides = sqrt(10). By Pythag Thm, remaining side is sqrt(15). Therefore half the required angle has tan = sqrt(10)/sqrt(15). Hence answer.

This way is the fast way. For tedious and more elegant expansions,

Let



Substitute mx+c into the equation, and for intersections delta = 0

Substitute c as to your resultant equation.

Then use the identity



Then use the angle between two lines form.

 

[deswa1]

Re: 2012 HSC MX1 Marathon

I got the answer in 1 minute. Unfortunately I'm hopeless in putting up a diagram. But I'll explain.

Circle is centered at origin with radius sqrt(10) and the external point (-3,4) has distance of 5 from the centre.{3,4,5} is a Pythagorean triple - so the 5 is immediate. Drawing the 2 tangents to the circle: consider 1 of the 2 congruent right-angled triangles: hypotenuse 5 and one of the shorter sides = sqrt(10). By Pythag Thm, remaining side is sqrt(15). Therefore half the required angle has tan = sqrt(10)/sqrt(15). Hence answer.

That is fantastic . I'm going to rep you for that.

 

[Kimyia]

Re: 2012 HSC MX1 Marathon

I'm terrible at graphing so could someone help me out with how to tackle this curve?
y = x^4 - 6x^2 + 8x +1
Thank you so much!!

 

[Carrotsticks]

Re: 2012 HSC MX1 Marathon

I'm terrible at graphing so could someone help me out with how to tackle this curve?
y = x^4 - 6x^2 + 8x +1
Thank you so much!!

You have no choice but to use the usual techniques ie: differentiate, let it = 0 for SP, let double derivative be 0 for POI etc etc.

Unless you have trouble with that as well.

 

[math man]

Re: 2012 HSC MX1 Marathon

I got the answer in 1 minute. Unfortunately I'm hopeless in putting up a diagram. But I'll explain.

Circle is centered at origin with radius sqrt(10) and the external point (-3,4) has distance of 5 from the centre.{3,4,5} is a Pythagorean triple - so the 5 is immediate. Drawing the 2 tangents to the circle: consider 1 of the 2 congruent right-angled triangles: hypotenuse 5 and one of the shorter sides = sqrt(10). By Pythag Thm, remaining side is sqrt(15). Therefore half the required angle has tan = sqrt(10)/sqrt(15). Hence answer.

This is what Drongoski's diagram would look like:

 

[Drongoski]

Re: 2012 HSC MX1 Marathon

This is what Drongoski's diagram would look like:
View attachment 24465

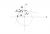
Thanks man. That's the diagram I would have loved to provide.

 

[Timske]

Re: 2012 HSC MX1 Marathon

y = e^x/(3 + e^x)

a. Show that f(x) has no stationary points.
b. Find the coodinates of the point of inflexion, given f '' (x) = [3e^x(3-e^x)]/(3+e^x)^3

 

[Carrotsticks]

Re: 2012 HSC MX1 Marathon

a) Differentiate it and show that y' = 0 has no solutions

b) Let f''(x) = 0 and solve for x.

 

[Timske]

Re: 2012 HSC MX1 Marathon

how would i find the inverse of y = e^x/(3 + e^x)

i get stuck on x(3+e^y) = e^y