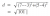Maths help (1 Viewer)

[Shazer2]

Over the course of the night I'm going to need some help with straight-line graphs. I'll be updating the thread each time I'm stuck.

See in later posts, for more problems.

 

[Manroop]

Its not the gradient the're referring to, its the distance between the 2 points.SO use distance formula instead! But you need to calculate gradient as well to show opps sides are parallel

 

[Shazer2]

I am so retarded, wow.

 

[twinklegal19]

Well you were right in that opposite sides are parallel, so those four points form a parallelogram. However in your working out, just because MQ and NP share the same gradient, it doesn't meant that they are equal based on just that.

In the answer, they found the lengths for all sides and it turned out that opposite sides were equal, which is just another test for a parallelogram.

 

[Demento1]

Well you were right in that opposite sides are parallel, so those four points form a parallelogram. However in your working out, just because MQ and NP have the same gradient doesn't meant that they are equal.

Listen to this. Find the distance of the two sides as well as the gradient which you have done.

 

[Shazer2]

Alright, I need some more help! I'm given the points A(0, 6), B(2, 0) and C(-2, 0). I need to show that perpendicular OA, where O is the origin, bisects BC. So, will I find the distance from (0, 6) to (0, 0) and then how do I determine if it bisects (2, 0)?

 

[twinklegal19]

Alright, I need some more help! I'm given the points A(0, 6), B(2, 0) and C(-2, 0). I need to show that perpendicular OA, where O is the origin, bisects BC. So, will I find the distance from (0, 6) to (0, 0) and then how do I determine if it bisects (2, 0)?

to find if it bisects BC, just find OB and OC, which are both 2

you don't need to find the distance AO

 

[Shazer2]

to find if it bisects BC, just find OB and OC, which are both 2

you don't need to find the distance AO

SO the distance for OB and OC is 2, how do I know that bisects BC? I'm so confused ._.

 

[twinklegal19]

SO the distance for OB and OC is 2, how do I know that bisects BC? I'm so confused ._.

well since OB and OC are equal, it means that AO cuts BC exactly in half.

try to draw a diagram if you still don't get it, it's really simple since the coordinates are on the axis

 

[Shazer2]

twinklegal19, how do I plot it in GeoGebra? What do I enter?

 

[twinklegal19]

twinklegal19, how do I plot it in GeoGebra? What do I enter?

um, I'm not experienced in plotting points on GeoGebra, but I'm sure there are other proficient fellow BOS-ers

Why not plot it on paper?

 

[Shazer2]

I'm still not sure how to plot on paper. What am I plotting? All I have so far is the distance for OB and OC.

 

[RealiseNothing]

Bisects just means cuts in half basically.

So if you have the distances of OB and OC, and if they are equal, then it is bisected.

 

[planino]

If a figure is a quadrilateral and has its opposite sides equal, doesn't it mean that it's a parallelogram? I'm under the impression that finding gradients are not required

(find out values using distance formula)
MO = NP = x

OP = MN = y

therefore opposite sides are equal

therefore MNOP is a parallelogram.

I could be wrong though. Your question is my question OP right now lol

 

[Shazer2]

So, I've plotted it like that, if someone can draw lines on it? xD

 

[twinklegal19]

If a figure is a quadrilateral and has its opposite sides equal, doesn't it mean that it's a parallelogram? I'm under the impression that finding gradients are not required

(find out values using distance formula)
MO = NP = x

OP = MN = y

therefore opposite sides are equal

therefore MNOP is a parallelogram.

I could be wrong though. Your question is my question OP right now lol

well there are more than one ways to prove a parallelogram in coordinate geometry, either by opposite angles are equal or parallel, ONE opposite pair of sides that are equal and parallel, or diagonals bisect each other (for that you can find their common midpoints)

View attachment 25634

So, I've plotted it like that, if someone can draw lines on it? xD

um it doesn't really matter now. You get that that OA bisects (cut in half) BC now, right?

 

[Shazer2]

Yes, I understand that now Alright, the next question. Find the exact length of the diameter of a circle with centre (-3, 4) if the circles passes through the point (7, 5).

I don't understand this at all, the wording throws me off completely. Can someone break it up for me and I'll see if I can go from there?

 

[planino]

find the distance between the centre and the given point (note, this is the circle's radius) using the distance formula.
Circumference = pi*diameter or 2*pi*radius.

Sub in your radius length into the
circcumference = 2*radius*pi formula

Since it asked for the EXACT length, leave your answer in terms of pi


The question could have been worded as 'the point (7,5) lies on the circle' rather than the 'circle passes through...'

 

[twinklegal19]

Yes, I understand that now Alright, the next question. Find the exact length of the diameter of a circle with centre (-3, 4) if the circles passes through the point (7, 5).

I don't understand this at all, the wording throws me off completely. Can someone break it up for me and I'll see if I can go from there?

Well if you think about it, any point on the circumference of the circle is always the same distance away from the centre, right? If you find the distance between that point which the circle passes through and the centre, you get the radius, which is half the diameter.

find the distance between the centre and the given point (note, this is the circle's radius) using the distance formula.
Circumference = pi*diameter or 2*pi*radius.

Sub in your radius length into the
circcumference = 2*radius*pi formula

Since it asked for the EXACT length, leave your answer in terms of pi

um the question is just asking for the diameter, which is two times the radius. You don't need the circumference formula, there is no pi in the solution

 

[Shazer2]

Aren't I finding the diameter? I won't need the circumference formula. I'll do:



Is that right?