complex locus (1 Viewer)
- Thread starter mabc1
- Start date
Since  , the equation can be rearranged to
, the equation can be rearranged to
 = 0)
Note that an argument of zero means that could be a positive real number
could be a positive real number  , as
, as  \implies z \neq 1 ) and any real
and any real  that is less than 1 produces a negative number with argument
that is less than 1 produces a negative number with argument 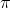 .
.
This means there are restrictions on the real and negative parts of .
.
Also, the identity^2 = (A+B)^2 - 4AB) might be useful.
might be useful.
The locus is not a circle, because as stated before any satisfies the equation.
satisfies the equation.
Note that an argument of zero means that
This means there are restrictions on the real and negative parts of
Also, the identity
The locus is not a circle, because as stated before any
Last edited:
for i) z-1/z^2 = a+0i, because arg is 0, therefore a number real. equate the imaginary part of the z-1/z^2 to 0 and get it into the form of a circle.
for ii) i think it creates a straight line; so simultaneously solve the line and the circle to get the intended values.
im too lazy to do it thou but thats how to solve it.
for ii) i think it creates a straight line; so simultaneously solve the line and the circle to get the intended values.
im too lazy to do it thou but thats how to solve it.
Last edited:
altSwift
Member
- Joined
- Jan 6, 2017
- Messages
- 65
- Gender
- Male
- HSC
- 2018
Can you pleaes explain how you rearranged it to getSince, the equation can be rearranged to
Note that an argument of zero means thatcould be a positive real number
, as
and any real
that is less than 1 produces a negative number with argument
.
This means there are restrictions on the real and negative parts of.
Also, the identitymight be useful.
The locus is not a circle, because as stated before anysatisfies the equation.
altSwift
Member
- Joined
- Jan 6, 2017
- Messages
- 65
- Gender
- Male
- HSC
- 2018
Ah thanks
Using,
Using,
 = 0\,\, (z \neq 0,\, 1))
