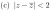Another one:
How would you graph this:
View attachment 41060
You can use
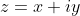
to show it rearranges to
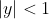
, and so is the region
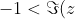} < 1)
.
However, thinking of the expression as a vector, the interpretation of the statement is:

is positioned such that the distance from
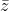
to

is less than 2 units
Since
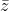
is located at the reflection of

in the real axis,
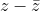
is a purely imaginary vector with its midpoint on the real axis.
So, if the length of this vector must be less than 2 units, then

must lie within 1 unit (vertically) from the real axis.
Thus, the region
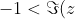} < 1)
covers all possible solutions for

.
---
These kinds of vector interpretations can make more algebraically complicated problems easier.
For example: Find the maximum value of
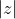
given that
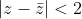
and
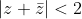
.
The answer is
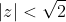
, arising from the four values
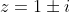
and
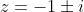
that correspond to the four corners of the square that defines the region within which

must lie.