Q10b and d pls
Attachments
-
2.3 MB Views: 30
Students helping students, join us in improving Bored of Studies by donating and supporting future students!

How do I simplify it from thereYou can simplify 10b and 10d to their sum and difference formulas.
View attachment 32579
Should be pre straightforward now. Construct triangles for each of the inverses, consider them alpha and beta respectively inside the sin(a+b) bracket and expand them how you would a regular sin(a+b) question, then construct the triangles for each of the separate functions and calculate respective values.
Here's an example of how it would like, for Q10b:
sin(sin^-1(4/5))cos(sin^-1(12/13) + cos(sin^-1(4/5)sin(sin^-1(12/13)
If you need more help, just reply and I can show the working out.
10B:How do I simplify it from there
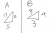
thank youOkay while your question is answered I would like to introduce an alternative here
