-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Discriminat-?! (1 Viewer)
- Thread starter epicFAILx
- Start date
The Derivative
Banned
if itz gratur den zer0, den there iz 2 s0lutionz 4 x.
Id itz less den zer0, it has one or no solutionz or sumting lyk dat idk.
Amiright? lol
~tbh, I have nfi
Id itz less den zer0, it has one or no solutionz or sumting lyk dat idk.
Amiright? lol
~tbh, I have nfi
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 847
- Gender
- Male
- HSC
- 2010
you can associate "discriminant" with the meaning of discriminating(distinguishing)
basically it tells the difference bewteen quadratics (actually polynomials of any degree, which you don't need to worry about)
when it's larger/equal to zero, the quadratic has real roots
when it's smaller than zeor, it has no real roots
basically it tells the difference bewteen quadratics (actually polynomials of any degree, which you don't need to worry about)
when it's larger/equal to zero, the quadratic has real roots
when it's smaller than zeor, it has no real roots
The Derivative
Banned
I basically said the same thing. hahayou can associate "discriminant" with the meaning of discriminating(distinguishing)
basically it tells the difference bewteen quadratics (actually polynomials of any degree, which you don't need to worry about)
when it's larger/equal to zero, the quadratic has real roots
when it's smaller than zeor, it has no real roots
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 847
- Gender
- Male
- HSC
- 2010
+1What are you finding hard about it? It's basically a part of the quadratic formula
it's related to the quadratic formula (which is derived from completing the square of the general equation of a quadratic ax^2 + bx + c= 0)
the solutions of ax^2 + bx + c= 0 are x= (-b+ sqrt(b^-4ac)) / 2a or x= (-b-sqrt(b^-4ac)) / 2a
so we'll need to find square root of a negative number if discriminant (b^-4ac) is smaller than 0, which doesn't exist in real numbers , so the quadratic has no real roots
otherwise, it has 2 real roots (which are obviously equal to each other when discriminant is 0)
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 847
- Gender
- Male
- HSC
- 2010
I basically said the same thing. haha
..speak english
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Let's see a basic quadratic function of:
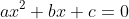
We all know what the quadratic formula is right?

Now, we call the discriminant the part under the square root.

So what if this "discriminant" is positive?
That is,

We get two different real solutions!
So what if the "discriminant" is equal to zero?
That is,

We get two equal real solutions!
So what if the "discriminant" is less than zero?
That is,

Since the discriminant is a negative when it is less than zero, and a square root of a negative number has no real solutions. We say it has no real solutions!
Try it yourself!
Use the normal way of solving it, then see how many solutions.
Then see if it matches with the discriminant.
Do the same with (for epicFAILx only):
a)
b)
c)
PM me for a list of exercises.
Note we usually call the discriminant . (Captial Greek letter for D.)
. (Captial Greek letter for D.)
So
We all know what the quadratic formula is right?
Now, we call the discriminant the part under the square root.
So what if this "discriminant" is positive?
That is,
We get two different real solutions!
So what if the "discriminant" is equal to zero?
That is,
We get two equal real solutions!
So what if the "discriminant" is less than zero?
That is,
Since the discriminant is a negative when it is less than zero, and a square root of a negative number has no real solutions. We say it has no real solutions!
Try it yourself!
Use the normal way of solving it, then see how many solutions.
Then see if it matches with the discriminant.
Do the same with (for epicFAILx only):
a)
b)
c)
PM me for a list of exercises.
Note we usually call the discriminant
So
Last edited:
ill try thoseLet's see a basic quadratic function of:
We all know what the quadratic formula is right?
Now, we call the discriminant the part under the square root.
So what if this "discriminant" is positive?
That is,
We get two different real solutions!
So what if the "discriminant" is equal to zero?
That is,
We get two equal real solutions!
So what if the "discriminant" is less than zero?
That is,
Since the discriminant is a negative when it is less than zero, and a square root of a negative number has no real solutions. We say it has no real solutions!
Try it yourself!
Use the normal way of solving it, then see how many solutions.
Then see if it matches with the discriminant.
Do the same with (for epicFAILx only):
a)
b)
c)
PM me for a list of exercises.
Note we usually call the discriminant. (Captial Greek letter for D.)
So
i sort of understand it now. But.. the question that is starting to really annoy me is:
Find the values of m such that the following quadratic equations have
(i) one root
(ii) two roots
a) x2 -mx + 2 = 0
.. the problem is.. what do you do with the m. It seems to throw me off
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
i) Remember what was said. When we have one root! We actually have 2 of the same solutions, eg. 8 and 8.
So referring back to what I have said.

Now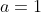 ,
,  ,
, 
So,^2 - 4(1)(2) = 0)


ii) Two roots = two different solutions
So what do we use? Yup,

Now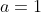 ,
,  ,
, 
^2 - 4(1)(2) > 0)

Have you learnt how to solve these inequalities? Draw a parabola! Part above it is,
 ,
, 
Note: Don't be afraid to try and make mistakes, that's the only way you can learn effectively.
So referring back to what I have said.
Now
So,
ii) Two roots = two different solutions
So what do we use? Yup,
Now
Have you learnt how to solve these inequalities? Draw a parabola! Part above it is,
Note: Don't be afraid to try and make mistakes, that's the only way you can learn effectively.
Last edited:
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 847
- Gender
- Male
- HSC
- 2010
find the discriminant as an expression involving mill try those
i sort of understand it now. But.. the question that is starting to really annoy me is:
Find the values of m such that the following quadratic equations have
(i) one root
(ii) two roots
a) x2 -mx + 2 = 0
.. the problem is.. what do you do with the m. It seems to throw me off
then solve the equation/inequality
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Also some questions asked especially in the 2U HSC exam is for which values of  are the roots rational/irrational, so learn this before moving ahead.
are the roots rational/irrational, so learn this before moving ahead.
someth1ng
Retired Nov '14
Basically, you use the [-b+/-sqrt(b^2-4ac)]/2aill try those
i sort of understand it now. But.. the question that is starting to really annoy me is:
Find the values of m such that the following quadratic equations have
(i) one root
(ii) two roots
a) x2 -mx + 2 = 0
.. the problem is.. what do you do with the m. It seems to throw me off
Substitute it all in with m and solve.
ie.
[-b+/-sqrt(b^2-4ac)]/2a=0 for one root
AND
[-b+/-sqrt(b^2-4ac)]/2a>0 for two roots
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Let me summarise for you epicFAILx.
So we said before
1. If , the quadratic equation has 2 REAL and UNEQUAL roots!
, the quadratic equation has 2 REAL and UNEQUAL roots!
This note can be divided into two sections,
a. If is also a perfect square, these two roots are RATIONAL!
is also a perfect square, these two roots are RATIONAL!
b. If is not a perfect square, these two roots are IRRATIONAL!
is not a perfect square, these two roots are IRRATIONAL!
2. If , then the quadratic equation has REAL and EQUAL roots!
, then the quadratic equation has REAL and EQUAL roots!
3. If , then the quadratic equal has NO REAL roots! [Note: It will have a complex root, which will be delt with in 4 Unit Mathematics.]
, then the quadratic equal has NO REAL roots! [Note: It will have a complex root, which will be delt with in 4 Unit Mathematics.]
Terms
- Real roots: They are just numerical solutions such as -1, 2, 2.1, etc...[So far throughout kindy and Year 11, we have used real numbers. Complex and imaginary numbers are used if you choose to do 4 Unit Mathematics.]
- Unequal roots: 8 and 7 are unequal roots. 6 and 1 are unequal, so on.
- Rational roots: Can be expressed in the form of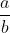
- Irrational roots: Cannot be expressed in the form of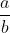
- Perfect square: Number that can be square rooted without a decimal answer. [Eg. 64, 100]
Also on occasions you will be asked for what values of has the quadratic have REAL SOLUTIONS.
has the quadratic have REAL SOLUTIONS.
When,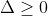
So we said before
1. If
This note can be divided into two sections,
a. If
b. If
2. If
3. If
Terms
- Real roots: They are just numerical solutions such as -1, 2, 2.1, etc...[So far throughout kindy and Year 11, we have used real numbers. Complex and imaginary numbers are used if you choose to do 4 Unit Mathematics.]
- Unequal roots: 8 and 7 are unequal roots. 6 and 1 are unequal, so on.
- Rational roots: Can be expressed in the form of
- Irrational roots: Cannot be expressed in the form of
- Perfect square: Number that can be square rooted without a decimal answer. [Eg. 64, 100]
Also on occasions you will be asked for what values of
When,
Last edited:
Oh My Gosh. SO its just simple substitution after finding out about the discriminant case (in this q)?!i) Remember what was said. When we have one root! We actually have 2 of the same solutions, eg. 8 and 8.
So referring back to what I have said.
Now,
,
So,
ii) Two roots = two different solutions
So what do we use? Yup,
Now,
,
Have you learnt how to solve these inequalities? Draw a parabola! Part above it is,
,
Note: Don't be afraid to try and make mistakes, that's the only way you can learn effectively.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Yes, that's all it is! Then of course you need to understand what you are actually doing. The Cambridge book has superb questions regarding the discriminant in Chapter 8. Go have a try if you have the Cambridge book. Have I confused you? If I have let me know, I can start from scratch if you need to.Oh My Gosh. SO its just simple substitution after finding out about the discriminant case (in this q)?!
Last edited:
4025808
Well-Known Member
Yes, also noting that if you're finding the roots in terms of x, then treat m as a constant like how you would treat numbers as constantsOh My Gosh. SO its just simple substitution after finding out about the discriminant case (in this q)?!
Edit: yay it's my 1100th post

