Hard enrichment question from the Cambridge textbook! (1 Viewer)
- Thread starter catha230
- Start date
In more concrete words, you are asked to show
given the conditions
 = 5,)
 = 5.)
So, try to solve for
. You have three equations with as many variables, so intuitively this should be solvable.
Bonus points - this question is not quite correct, because there are other values of that work too. Can you find them?
This is a possible (but long-winded) solution. Probably not the intended one?
given the conditions
So, try to solve for
Bonus points - this question is not quite correct, because there are other values of
This is a possible (but long-winded) solution. Probably not the intended one?
From the last two equations, 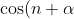 = \cos (2n+\alpha))
, so we have (by the general solutions to trig equations)
,)
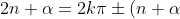or 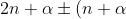= 2k\pi,)
for some integer 
.
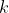
So either
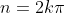
or 
.
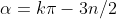
The former implies that 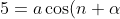= a \cos (2\pi+\alpha) =a \cos \alpha = 1)
, so it cannot be true.
Looking at the first two equations,
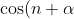 = 5 \cos \alpha,)
so
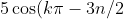 - \cos (k\pi - n/2) = 0)
.
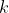
Now changing can only flip the sign of the LHS, since  )
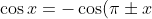. Because we really only care about 
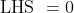
, we can just pick 
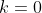
for simplicity. Make the substitution 
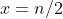
to get
.
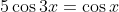
We can expand the LHS using angle sum formulae. Then use
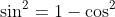
to write everything in powers of 
:
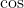
Now
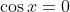
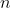
cannot be true, otherwise would be an odd multiple of 
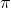
and so 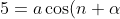 = a \cos (\pi + (2k\pi+\alpha)) =-a \cos \alpha = -1 )
.
Thus
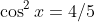
and so
)
.
for any integer.
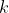
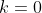
The positive case with is numerically equivalent to  )
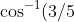. Put these in a calculator to convince yourself this is true (or even better, try proving it).
At this point we're done, but if you want to graph these results you can solve for
by using 
.
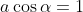
or
So either
The former implies that
Looking at the first two equations,
so
Now changing
We can expand the LHS using angle sum formulae. Then use
Now
Thus
for any integer
The positive case with
At this point we're done, but if you want to graph these results you can solve for
Last edited: