^{n} = (1+x)^{n}(1-x)^{n})
using the binomial theorem:
 + \binom{n}{2}(-x^2)^2 + ... + \binom{n}{n-1}(-x^2)^{n-1} = \left [\binom{n}{0} + \binom{n}{1}x + \binom{n}{2}x^2 + ... + \binom{n}{n-2}x^{n-1} + \binom{n}{n}x^n} \right ]\left [\binom{n}{0} - \binom{n}{1}x + \binom{n}{2}x^2 + ... + (-1)^{n-1})\binom{n}{n-2}x^{n-1} + (-1)^{n}\binom{n}{n}x^n} \right ])
We must now equate the coefficients of
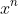
on both sides, but in order to do this, we must take 2 cases.
Case 1: n is odd
if n is odd, on the LHS there is NO TERM for
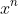
, ie the coefficient of
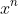
is 0. This is because on the LHS only x to the power of an even number exists (
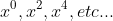
) since the powers are integers multiplied by 2. Thus the coefificient to x to the power of an odd number on teh LHS will always be 0. Thus teh coefficient of
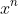
, is 0 on the LHS.
However on the RHS, the coefficient of
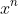
is attained by multiplying the coefficient of
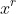
by the coefficient of
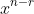
, where
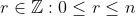
ie coefficient of
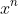
on the RHS (starting by multiplying the last coefficient in teh first bracket by the first coefficient in the last bracket, etc.) =

[note - since n is odd, the last term will definitely by negative, the 2nd last will definitely be positive, etc as shown]
but
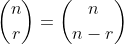

 Case 2: n is even
Case 2: n is even
now if n is even, we have the same RHS for the coeffivient of
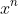
but on the LHS, since n is an even integer,
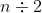
is an integer, and thus the term with
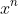
on the LHS is NOT 0, but rather:
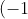^{n\div 2}\binom{n}{n\div 2}(x^2)^{n\div 2} = (-1)^{n\div 2}\binom{n}{n\div 2}x^n)
thus the coefficient of
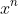
on the LHS is:
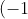^{n\div 2}\binom{n}{n\div 2} = \frac{(-1)^{n/2}n!}{(n-{n/2})!(n/2)!)} = \frac{(-1)^{n/2}n!}{((n/2)!)^2})
equating the coeffieicnt of
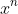
on the LHS and RHS for n even, we have:
^{n/2}n!}{((n/2)!)^2} = \frac{\frac{(-1)^{n/2}n!}{(n/2)!}}{(n/2)!} = \frac{(-1)^{n/2}{\left [ ({n/2}+1})(n/2+2)(n/2+3)...(n))\right]}{(n/2)!} = \frac{2}{2}\times \frac{(-1)^{n/2}{\left [ ({n/2}+1})(n/2+2)(n/2+3)...(n))\right]}{1\times 2\times 3\times ...\times n/2} = \frac{(-1)^{n/2}{\left [(n+2)(n+4)(n+6)...(2n))\right]}} {2\times 4\times 6\times ...\times n})
as required
MAN THAT WAS A B**** TO WRITE OUT!!! lol
i still dont get why they say "show that...when n is even, its value is: [and then gives 2 expressions, i really think they should just get you to show the RHS of that expression....]

