The remainder theorem tells that the remainder when a polynomial
)
is divided by
)
is
)
.
Applying this to the statement that "When P(x) is divisible by (x+1) the remainder is -11" tells us that:
We have divided by
 \equiv (x - \alpha) \quad \implies \quad \alpha = -1)
Thus, the remainder is
)
which, the question tells us, is
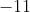
, and so
 &= -11 \\ (-1+1)(-1-3)Q(-1) + a(-1+1) + b &= -11 \qquad \qquad \text{since $P(x) = (x+1)(x-3)Q(x) + a(x+1) + b$} \\ 0 \times -4 \times Q(-1) + a \times 0 + b &= -11 \\ b&= -11 \end{align*})
Applying the same technique to the statement about dividing by
)
should yield the value of

.
Now, the division algorithm tells us that if I divide a polynomial
)
by another polynomial
)
(the divisor), where
)
is of the same or lesser degree than
)
, then the result will be a quotient,
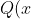)
, and a remainder,
)
. The quotient will have a degree that is no greater than the difference in the degree of
)
and
)
and the remainder will have a degree no higher than one less than that of
)
. This gives us the formula
 = d(x)Q(x) + R(x))
Using a concrete example, suppose I have a polynomial
)
of degree 5 (say) and I divide it by
 = x - 1)
, then I will get a quotient
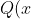)
of degree no more than 4 and a remainder
)
of degree no more than 0 (as the degree of
 = x - 1)
is 1). In other words,
)
will be a constant (
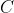
, say).
 = (x - 1)Q(x) + C)
This shows why the remainder theorem works, and also the factor theorem (if

is a root of
)
then
)
is a factor, and thus
 = 0)
.
Now, if I divide a polynomial by a divisor that is of degree 2 - something like
 = kx^2 + mx + n)
, or
 = x(x - 5))
, or
 = p(x - \alpha)(x - \beta))
), then the remainder will be of at most degree 1, and so be in the form
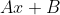
.
 = (kx^2 + mx + n)Q(x) + Ax + B)
and this is the situation you have here. On division of
 = (x+1)(x-3)Q(x) + a(x+1) + b)
by
(x-3))
, the quotient will be
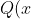)
and the remainder will be the degree 1 polynomial
 = a(x+1) + b)
(or it could be a degree 0 polynomial, depending on the value of

), which you can simplify easily once you have found the values of

and
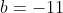
.
I get the remainder as
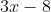
, FYI.

