I recall doing the 2nd question late last year.
The basic idea is very simple. Say if you draw a right-angled triangle ABC, right-angled at B, with hypotenuse of length 7 say, then the 2 shorter sides are AB = 7 cos A and BC = 7 sin A.
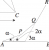
Now for this question, form the 3 right angled triangles with hypotenuses AP, PQ and QR (each of length x, say) resp., with their shorter sides parallel to, and vertical to side AB respectively. Also drop the perpendicular to line AB from R, meeting AB at Z say.
Then tan(angle BAR) = RZ/AZ
Now RZ is the sum of the vertcal sides of the 3-right angled triangles, and
AZ is the sum of the 3 horizontal sides. Therefore:
RZ = x sin @ + x sin 2@ + x sin 3@ = x (sin@ + sin 2@ + sin 3@)
AZ = xcos @ + x cos 2@ + x cos 3@ = x (cos @ + cos 2@ + cos 3@)
Hence the result.