I think so.
By symmetry considerations, it suffices to show that for z > 0, and (x,y,z) a point on the hyperbolic paraboloid
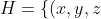:z=\frac{x^2}{a^2}-\frac{y^2}{b^2}\})
that there exists exactly two (up to rescaling) nonzero triples (u,v,w) such that the line
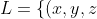+t(u,v,w):t\in\mathbb{R}\})
entirely lies in H yes?
From standard mx2 conics, we can parametrise points on H in terms of the variables
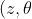)
as
)
If L is to lie in H, we require for any real t that
^2}{a^2}-\frac{(b\sqrt{z}\tan\theta+tv)^2}{b^2}=z+tw.)
Expanding this out we get a quadratic:
+2\sqrt{z}t(\frac{u\sec\theta}{a}-\frac{v\tan\theta}{b}-\frac{w}{2\sqrt{z}})=0.)
This polynomial identically vanishes iff its coefficients are both zero.
The leading term tells us
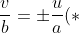.)
Now if w=0, this identity together with setting the linear coefficient in the t-polynomial to be zero leads to the statement u=v=w=0, which does not give us a "ruling line".
On the other hand, if w is nonzero, by rescaling we might as well assume
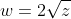
.
This leaves us with
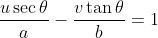
, which together with (*) lets us solve for u and v.
We get two solution pairs depending on our choice of sign.
Pretty sure this does it, (we haven't treated the z=0 case, but nothing goes wrong here...we are just forced to have w=0 and together with (*) this once again gives us our two ruling lines.)
entirely lies in H yes?
as
.
, which together with (*) lets us solve for u and v.
