Integral Calculus (1 Viewer)

[csi]

Hi guys,

I have a couple of questions that I need help with:

1. Find d/dx ∫8~x (2t^5 - 3)^6 dt.
Answer: (2x^5-3)^6

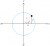
2. Find ∫3√2~6 √(36-x^2) dx by using the formula for area of a segment.
Answer: 9(π/2-1)

Note: ∫a number ~ another number are the limits of the integration.

Thanks

 

[cossine]

For q1 the upper bound doesn't matter as the derivative of a constant is zero.

So an equivalent question is:

- d/dx integral (2x^5-3)^6 dx

As differentiation and integration are inverse operations the result is -(2x^5-3)^6

For q2 try the substitution 6sin(u) = x

You can then use the theorems cos^2(theta) = ( 1+cos(2*theta) )/2 ** and 1-sin^2(theta) = cos^2(theta).

**Similar theorem sin^2(theta) = ( 1- cos(2*theta) )/2

https://www.integral-calculator.com/

 

[imaiyuki]

hi, i haven't really touched on integration much yet, but here's my take

1. this is basically just requiring you to recall the fundamental theorem of calculus, i.e.
where A(x) is the signed area function.
If you need a proof, here's a screenshot from my upcoming 2u maths notes!

so as you can see it really doesn't matter what the lower bound is, as long as it fits the mould of a~x where a is constant then the result will always be f(x) as per the answer.

2. the first hint as to what you need to do comes from the weird lower bound, so first thing i thought was to do some trig:
construct a triangle of 45˚ on the right side like this, but with radius=6.

Using trigonometry we find that
and thus through some manipulation and rationalising denominator, x=3√2
therefore we know that the area we want is 1/8 of the circle minus the triangle.
circle area is 36pi, therefore 1/8 would be (9/2)pi, and the triangle area can be found by 1/2(absinC) (of course you could find y, but im lazy)
therefore triangle area = 9
And thus we get 9(π/2-1)