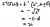Average Boreduser
Rising Renewal
don't these result in -x given the restriction for f(x)?
I got the inv function to be -sqrt(x) basing it from the original graph of f(x)
I got an Idea on why it might be wrong (can ya'll confirm if I'm right?):
as f(x) is restricted to x<=0, we can simplify the function to sqrtx- when we find the inverse, f^-1(x) will = x^2. Hence, we can prove the two identities
^reason why I'm asking is bc I get abs(x) If I implement it, seems flawed
I got the inv function to be -sqrt(x) basing it from the original graph of f(x)
I got an Idea on why it might be wrong (can ya'll confirm if I'm right?):
as f(x) is restricted to x<=0, we can simplify the function to sqrtx- when we find the inverse, f^-1(x) will = x^2. Hence, we can prove the two identities
^reason why I'm asking is bc I get abs(x) If I implement it, seems flawed
Last edited: