pwoh
O_O
Yr 12 Cambridge, 1A, Question 20.
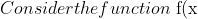 = \frac{1}{6}(x^2-4x+24)\\...\\$(e) Let $ N $ be a negative real number. Find f^{-1}(f(N)))
The answer is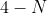 but I don't understand why.
but I don't understand why. 
Also, how would you: "Prove, both geometrically and algebraically, that if an odd function has an inverse function, then that inverse function is also odd."?
Thanks
The answer is
Also, how would you: "Prove, both geometrically and algebraically, that if an odd function has an inverse function, then that inverse function is also odd."?
Thanks
Last edited:
