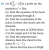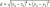Here is the solution to Q10 they should be right.
Fractions are in brackets eg. (1/2).
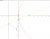
It really helps if you do a sketch of the information for these questions. Mine are attached.
Can you screenshot all of Q5 as part h) isn't making sense on its own.
Hope this helps.
Question 10: y^2 = 20x
a) Find the equation of the chord FR, where F is the focus
focus is (a,0)
y^2=4ax therefore 20=4a so a = 5
F= (5,0)
m(FR) = 0-(-2)/5-(1/5)
m(FR) = 5/12
equation of chord: y-0=(5/12).(x-5)
simplifies to 5x-12y-25=0
b) x= -5 is equation of directrix
substitute x=-5 into 5x-12y-25=0
-25-12y-25=0
therefore y=-4(1/6)
Q=[-5, -4(1/6)]
c) base = OF = 5
height = 4(1/6) as O and F are both on the x-axis and Q is 4(1/6) units below this
therefore by calculation the area of triangle OFQ = 10(5/12) units^2
d) pd = |ax1 + by1 + c|/(a^2 + b^2)^(1/2)
use equation of chord in general form 5x-12y-25=0 thus a=5 b= -12 c= -25
P(-1,-7) x1 = -1 y1 = -7
substitute into formula to get the distance as 4(2/13)
e) Note: R and Q lie on the same line, the chord 5x-12y-25=0.
Hence pd calculated above is the height of the triangle
The base is the distance between R and Q - use distance formula answer is 5(19/30)
Therefore area of triangle PQR = 11.7 units^2