I think that the last one is a 4u question only but used to be 3u.
7)
Nevertheless, the first one I think might be C.
This is because we see a double root at x=-2 for f'(x). That means f(x) must have x=-2 as a triple root. This means
^3)
is a factor. Hence A and B are eliminated. From here, it's obvious it's C. f'(x) never hits the x-axis again as x approaches negative infinity, meaning f(x) has no turning points back there, hence it cant have another root below 0. Similarly, it cant have a root between 0 and 4 because there are no turning points there either. Therefore, it must have a root at x=6, meaning (x-6) is a factor. Hence, the only possible roots in the options available that f(x) could have is C.
8)
Next one I prefer using implicit differentiation.
Basically, just differentiate everything in terms of x. Note the ys become y' times their differential. The first term is a product, so you use the product rule.
 + x\frac{dy}{dx}) - 2x + 4y^4\frac{dy}{dx} + 0 = 0 )
Make the
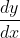
the subject and simplify, you'll get

Sub in the point you get

So the gradient is 1.
Point-gradient formula:
)

So answer is B.
Please correct me if I got it wrong.
9)
For the last one, straight away I would sub in the initial condition for all options.
Doing this will eliminate C and D instantly because neither

nor

is correct.
Next easiest thing to do is employ the formula:
 = a)
It's a bit of a pain but the easier one to do imo is A. If you dont know the method, square the equation, halve, then differentiare W.R.T x. Doing this youll get a = 8 which is wrong so it must be B.




