Maths help (1 Viewer)

[Farhanthestudent005]

Please help. Will appreciate it . Thanks

 

[icycledough]

It would help to use Newton's Law of Cooling (which is T = T0 + Ce^-kt); T0 would be -10 (temperature of freezer), then to find C, you sub in t = 0 and T = 14 (initial temperature). Then use t = 25 and T = 11 to find k. Then once you have the whole formula, you should be able to do a) and b).

For a), sub in t = 300 (REMEMBER, we are using seconds, so everything must be same units; alternatively, you can use minutes, but it is more tedious)

For b), sub in T = -8 and find the value of t

 

[CM_Tutor]

You can also solve this starting directly from Newton's Law of Heating and Cooling, which states that the rate of change of the temperature of an object is proportional to the difference between its temperature and that of its surroundings.

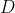
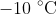
So, let be the difference between the temperature of the piece of meat and the temperature of its surroundings (which we know is . It follows that the temperature is decreasing and so

​

The solution of this differential equation is

​

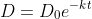
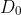
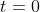
where is the temperature difference at , and thus .

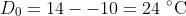
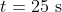
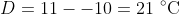
We are given the constraint that, at , and so:

​

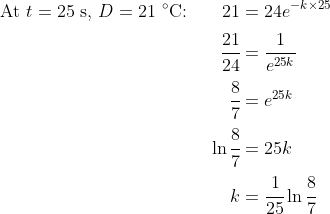
So, after 5 min (300 s), the temperature difference is:

​

So, the temperature after 5 minutes is:

​

And, the temperature will reach when:

​