Show that the point
)
lies on the line joining
)
and
)
and find the ratio in which is divides
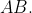
First we must find the equation of
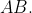
We can always find the gradient,
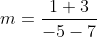
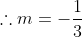
Now, we use a infamous Year 8 formula,
)
)
Simplify!
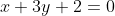
We must test to see if the equation holds true at point P. Testing
,)
+2=0)
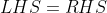
Hence
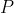
lies on the interval
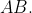
There is one thing we must do before attempting this question, actually, two things. We must first understand if it is an internal or external division. Then we must understand what we are actually doing when doing division of an interval.
Drawing a pretty diagram will help this cause!

From our pretty diagram, it is obviously an internal division! So no minuses involved. We can also see that obviously by similar triangles,
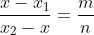
Similarly,
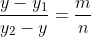
Ah, now if we simplify each expansion we get our division formula! But we do not want to do so because, we have what we need.
Just substitute our values inside! One of the equations! Let's pick first since first is the best and good for your ATAR.
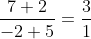
Horaay! Therefore the ratio that
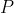
divides
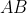
is in,
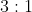
You must understand the underlying concept of ratio division! No rote learning!

