Optimisation and MAX \ MIN questions are very common. There has been one on every 2u / Advanced HSC since 1980, and most trial (and many half-yearly) papers have one as well. Some come with a lot of structure, some with little, which has benefits and drawbacks. I believe every student needs to be aware that these questions fall into broad types and virtually all can be answering with the same approach:
- Set up the problem, usually involving drawing an appropriate diagram and properly defining variables.
- Form an equation for the quantity that you seek to maximise / minimise - area in the above example.
- Usually this equation will have more than two variables, so examine the problem for additional (unused) information that will allow you to eliminate one of the variables.
- Find the maxima / minima, usually by calculus, by sometimes by other methods (such as for the vertex in the above case).
- MAKE SURE that you establish that they are maxima or minima and not just assume. This is typically done by considering the sign on the first derivative around the stationary points, or by testing the second derivative, but it need not be done this way - any VALID proof of nature is fine.
- Before giving a final answer, consider whether you have a restricted domain and thus need to consider the possibility of a maximum or minimum value located at an end point. MAKE SURE that you do actually ANSWER THE QUESTION by providing whatever is asked, and remember not to answer using any variables that you have defined.
In the above case, a maxima at a vertex of a parabola, the global maximum was also there given the shape of the curve. Thus, consideration of end points was not needed.
I hope that you can see that my solution follows this structure, and it is applicable to virtually all MAX/MIN problems that I have seen.
Extension: If we had been asked for the minimum area, however, the domain would have been needed. The restrictions must (at least) be that

and

, being lengths, can't be negative, and since the perimeter requirement tells us that
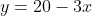
, we have
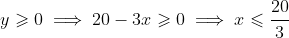
and
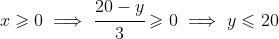
.
Now, by combining these, we get:
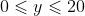
and
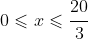
.
Further, as
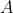
also can't be negative, we cna find another set of restrictions on

:
x^2 + 40x \\ &\implies 0 \leqslant x \leqslant \cfrac{40}{6 - \sqrt{3}} = \cfrac{40\left(6 + \sqrt{3}\right)}{33} \end{align*})
This is a broader domain than was established above by prohibiting

or

from being negative, however, so does not impose any additional conditions.
Now, let's consider
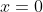
:
 \times 0^2 + 40(0) = 0)
but... is this a reasonable answer? After all, if
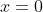
and consequently
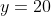
, out "house" shape has no equilateral triangle at the top, and no base... it is simply a 40 unit length bent in half to be two overlapping 20 unit "walls".
At
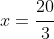
, which corresponds to
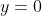
and thus our "house" being an equilateral triangle:
 \times \left(\cfrac{20}{3}\right)^2 + 40\left(\cfrac{20}{3}\right) \\ &= \cfrac{400\left(\sqrt{3} - 6\right)}{9} + \cfrac{800}{3} \\ &= 400\left(\cfrac{\left(\sqrt{3} - 6\right) + 2 \times 3}{9}\right) \\ &= \cfrac{400\sqrt{3}}{9}\ \text{units}^2 \end{align*})
Assuming we require an actual house shape (i.e.
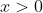
and
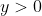
), the smallest possible house will have the longest possible walls and the smallest possible triangle, and thus will have an

that is as close as practicable to 0, whilst still being positive, and walls as close as practicable to, but still below, 20 units in length, producing a positive total area that can be made as close to zero as might be sought.
