perms and combs qn (1 Viewer)

[Masaken]

how would you do this with perms and combs? the worked solutions are using a probability tree and i think there's probably an easier way to go about this question, many thanks in advance

 

[jimmysmith560]

The total number of ways can be given by

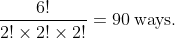
Excluding arrangements where letters that are next to each other are identical from total arrangements results in the arrangements where no identical letters are next to one another. There are 3 situations where identical letters are next to one another:

• All 3 pairs together
• Only 2 pairs together
• Only 1 pair together

Having all three pairs next to one another can be expressed as A, A, B, B, C, C (just like in the question). In this case, the number of arrangements is

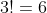
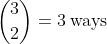
Having only 2 pairs next to one another can be expressed as C, A, A, B, B, C. The 2 pairs to be together can be selected in , with the third pair being the one where letters are not next to each other. The 2 chosen pairs can swap their places, causing 2 arrangements, each letter from the third pair can be placed in 3 positions, resulting in

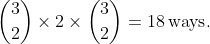
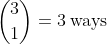
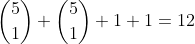
Having only 1 pair together (i.e. the other 2 pairs of identical letters will not be next to one another) means that there are to choose a pair of identical letters to be next to one another. On this basis, the number of placements for one pair of identical letters (for example, A) is . When considering all three pairs, this number becomes

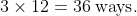
The rest involves adding 6, 18 and 36 (resulting in 60) and subtracting this sum from 90, resulting in 30.

I hope this helps!