Could someone possibly explain to me the steps of this from how they converted the sum into the sum product thingy up until they get 1/n?
The sum
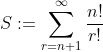
in expanded form is just
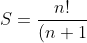!}+\frac{n!}{(n+2)!}+\frac{n!}{(n+3)!}+\cdots)
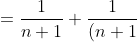(n+2)}+\frac{1}{(n+1)(n+2)(n+3)}+\cdots)
.
Now this last series is an infinite series clearly, and the
rth term in the series is just
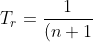(n+2)(n+3)\cdots (n+r)}=\prod_{j=1}^{r}\frac{1}{n+j})
.
So that infinite series is
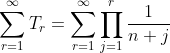
, which is what the working out got.
The next step (the inequality) is clear: the general term of the series on the RHS has
r "(
n+1)" factors on the denominator, and each of these is LESS than or equal to the
r factors in the general term (
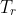
) of the denominator of series in the LHS, so the overall fraction on the RHS is GREATER than that in the LHS.
After that, just use infinite geometric series formula for common ratio less than 1.