the diagram is not to scale therefore impossibru to tell
trick question nice one m8
The question definitely has an answer. The triangle
ABC is a unique one in shape, since we know all its angles (it's an isosceles triangle with base angle 80°), and there is only one point
E on
BC such that ∠
BAE = 70°, so point
E is fixed with respect to Δ
ABC. Also, point
D is fixed, as there is only one point on
AC such that ∠
ABD = 60°. Therefore, ∠
AED is fixed, i.e. a single value for
x exists. We find this value below.
Without loss of generality, let
AB = 1. Using the fact that the angle sum of a triangle is 180°, we note that ∠
AEB = 30° (from Δ
AEB), ∠
ADB = 40° (from Δ
ABD) and hence ∠
BDE = 130° –
x (from Δ
BDE).
By the sine rule in Δ
BDE,
}=\frac{BD}{\sin (30^\circ + x)})
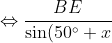}=\frac{BD}{\sin (30^\circ + x)})
, since sin(130° –
x) = sin[180° – (130° –
x)] = sin(50° +
x).
}{\sin (50 ^\circ + x)}=\frac{BD}{BE} \text{ }(\ast))
.
By the sine rule in Δ
ABD,
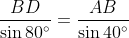
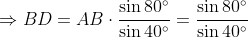
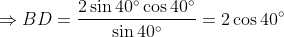
(by the double angle formula for sine).
By the sine rule in Δ
BEA,
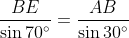
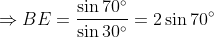
(as
AB = 1 and cosec 30° = 2)
Substituting the values for
BD and
BE into Equation (*),
}{\sin (50 ^\circ + x)}=\frac{BD}{BE})
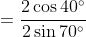
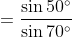
, as cos 40° = sin(90° – 40°) = sin 50°
i.e.
}{\sin (50 ^\circ + x)}= \frac{\sin 50^\circ}{\sin 70 ^\circ})
.
It is clear that the LHS above becomes the RHS when
x = 20°. If
x = 20° is the only possible solution given the circumstances, the answer is
x = 20°. We show that this is indeed the case.
Firstly, note that 0° <
x < 70°. To see this, let
D′ be the point on
CB such that
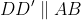
.
Then by alternate angles in parallel lines
DD′ and
AB, ∠
D′
DB = ∠
ABD = 60°. Then by angle sum of Δ
BDE, we have
(
x + 30°) + 20° + (60° + ∠
EDD′) = 180° (as ∠
BDE = 60° + ∠
EDD′)
⇒
x + ∠
EDD′ = 70°
⇒ 0° <
x < 70°.
Now, consider
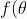:=\frac{\sin (30^\circ + \theta)}{\sin(50^\circ + \theta)}, \text{ for }\theta \in (0^\circ, 70^\circ))
. The function is defined for all
θ in the given domain.
Also,
=\frac{\cos (30^\circ + \theta)\sin(50^\circ + \theta)-\sin(30^\circ + \theta)\cos(50^\circ + \theta)}{\sin^2(50^\circ + \theta)})
-(30^\circ + \theta)]}{\sin^2(50^\circ + \theta)})
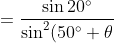})
)
.
Therefore,
f(
θ) is an increasing function (and hence one-to-one) for all
θ in the given domain, so there can only be one solution to Equation (*), as 0° <
x < 70°. As
x = 20° is a solution, it is the only solution, and hence the answer to the original problem.


