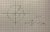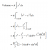The circle x^2 +y^2 = r^2 has radius r and centre O. The circle meets the positive x-axis at B. The point A is on the interval OB. A vertical line through A meets the circle at P. Let Theta=angle OPA.
The shaded region bounded by the arc PB and intervals AB and AP is rotated about the x-axis. Show that the volume V formed is given by
V= ((π r^3)/3)(2 - 3sin Θ + sin^3 Θ)
Having a bit of trouble with this one. I've tried to find A in terms of theta (using trig) for the definite integral but have come upon nothing. I'm sure there's probably a key rule or identity or something which I'm missing, either that or I've interpreted the sketch wrong. Maybe I'm just too sleepy. Any help is appreciated thank you

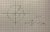
The shaded region bounded by the arc PB and intervals AB and AP is rotated about the x-axis. Show that the volume V formed is given by
V= ((π r^3)/3)(2 - 3sin Θ + sin^3 Θ)
Having a bit of trouble with this one. I've tried to find A in terms of theta (using trig) for the definite integral but have come upon nothing. I'm sure there's probably a key rule or identity or something which I'm missing, either that or I've interpreted the sketch wrong. Maybe I'm just too sleepy. Any help is appreciated thank you