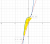
Volumes of rotation (1 Viewer)

[=)(=]

For some reason I cant get part c

 

[5uckerberg]

Okay, so the idea is that your shape will resemble a cone or in many of these cases the outside surface of the cone. The tangent from Q20a is .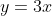

Now the concept of integrating is to find the section under the curve.

Combining Q20a and what we know you are integrating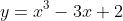 . Now when you are finding the volume of several boundaries you are simply finding the volume of a cone.

When you are rotating around the x-axis you are treating the height of x as Infinitismal height which then becomes dx and then the radius of the cone is y so you are working with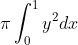 . To finish this off sub the equation for y and use reverse chain rule. Note the boundaries represent the height of the structure.

Similarly rotation around the y-axis implies that you treat the y-axis as height and the x-axis as radius.

For part b there is a clever way of doing the question. Find the volume of the solid formed when the region is rotated around the y-axis for just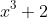 take away the volume from .

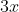For part b you are working with

 

[=)(=]

Are you finding the volume of this shaded region?

 

[5uckerberg]

Are you finding the volume of this shaded region?
View attachment 34957

Remove everything that is the left of the y-axis. As you are finding the region between the curve and tangent and the y-axis.
This is a vital part for part c.

 

[=)(=]

ohh so the volume of this triangular shaped region

 

[5uckerberg]

That is what I think the question is asking.

 

[=)(=]

That is what I think the question is asking.

ohh okay makes sense thank you