Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
The exact question:
The point P(x, y) is equidistant from the lines:
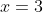
And
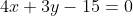
Find the locus of point P.
What I did:
Let variable point
A vary on x=3
Therefore the coordinates of A are:
A(3, y)
Let a variable point
B vary on the line 4x+3y-15=0
Therefore the coordinates of B are:
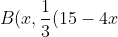) )
Lets take the distance formula of PA and PB, simplify all on to one side using our knowledge that PA=PB
Simplify, hence locus of P (I got a big expression with x^2 and y^2 and x and y etc.)
Apparently the locus is a striaght line(s)
I can see how this is, but the method you are supposed to do assumes perpendicular distance. If it said perpendicular distance then its easy and I know what to do, but the wording is vague and I want to know why my solution is mathematically incorrect (as far as I can tell, it definitely answers the question)
Thanks
The point P(x, y) is equidistant from the lines:
And
Find the locus of point P.
What I did:
Let variable point
A vary on x=3
Therefore the coordinates of A are:
A(3, y)
Let a variable point
B vary on the line 4x+3y-15=0
Therefore the coordinates of B are:
Lets take the distance formula of PA and PB, simplify all on to one side using our knowledge that PA=PB
Simplify, hence locus of P (I got a big expression with x^2 and y^2 and x and y etc.)
Apparently the locus is a striaght line(s)
I can see how this is, but the method you are supposed to do assumes perpendicular distance. If it said perpendicular distance then its easy and I know what to do, but the wording is vague and I want to know why my solution is mathematically incorrect (as far as I can tell, it definitely answers the question)
Thanks
Last edited:

