tacogym27101990
Member
hey
im a little bit rusty at complex, can someone please give me a bit hint as to how to solve this?
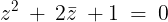
thanks
im a little bit rusty at complex, can someone please give me a bit hint as to how to solve this?
thanks
Last edited:
