lol haha. This is coming from the guy that told ppl to study for non-uniform circular motion.
There is one little bit in the syllabus that requires you to consider non uniform circular motion when proving the tangential and normal components of circular motion.
Anyway, check out 10.5 of the current 2U/3U syllabus. It states:
Other considerations are symmetry about the axes,
behaviour for very large positive and negative values of x, and the points at which functions such as:

The second curve has an oblique asymptote (at y=x).
So, although it doesn't specifically mention the word "oblique asymptote", I think that it's pretty reasonable to say that oblique asymptotes could very well be examined in the HSC, even at 2U level since it was not marked as an extension topic.
Furthermore, I'm not familiar with the Year 11 2U course. But I'm pretty sure that limits of functions are included. So although the syllabus specifically marks the finding of horizontal and vertical asymptotes as Ext 1 material, they very well could ask in a curve sketching question, in my opinion, to find the limit of the equation of the curve as
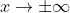
in a previous part. This would mean that you would have to mark a horizontal asymptote if they ask you to sketch the curve showing "the above" features.
But this would mean that at 2U level they couldn't ask something like "Find the horizontal and vertical asymptotes of ..."
This would be similiar to the approach they take in Ext 2 partial fractions regarding repeated linear factors.
