Yeah my bad lol. Sorryi dont see it
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
4 Unit Revising Marathon HSC '10 (1 Viewer)
- Thread starter jet
- Start date
A group of 7 boys and 5 girls go to watch a movie together.
(i) In how many ways can they sit in a row if the boys sit together and the girls sit together?
(ii) In how many ways can they sit together in a row if no two girls are to sit together?
(iii) After the movie the group of twelve go to a café and sit at a round table so that two particular girls sit together, five particular boys sit together, the remaining three girls sit together and the remaining two boys sit together. The four groups around the table don't mind which other group they are seated next to and within each group no one minds who they sit next to. In how many different ways can they be arranged?
(i) In how many ways can they sit in a row if the boys sit together and the girls sit together?
(ii) In how many ways can they sit together in a row if no two girls are to sit together?
(iii) After the movie the group of twelve go to a café and sit at a round table so that two particular girls sit together, five particular boys sit together, the remaining three girls sit together and the remaining two boys sit together. The four groups around the table don't mind which other group they are seated next to and within each group no one minds who they sit next to. In how many different ways can they be arranged?
Pwnage101
Moderator
How about we give the '10er's a go to answer/ask these Q's...
i) 7P7 x 5P5 x 2 o-oA group of 7 boys and 5 girls go to watch a movie together.
(i) In how many ways can they sit in a row if the boys sit together and the girls sit together?
(ii) In how many ways can they sit together in a row if no two girls are to sit together?
(iii) After the movie the group of twelve go to a café and sit at a round table so that two particular girls sit together, five particular boys sit together, the remaining three girls sit together and the remaining two boys sit together. The four groups around the table don't mind which other group they are seated next to and within each group no one minds who they sit next to. In how many different ways can they be arranged?
ii) 7P5 x 5P5 x2 + 5P5 x 7P4 x2
dont wna embarass myself now .. correcy me if you want xD
Just a question when do you use P and C. C = order important? P = order not?
Last edited:
i) Sn = (w^n-1)/(w-1) or is it(i) Find the sum 1 + w + w2 + w3 +... to n terms, considering the cases n=3k, n=3k+1, n=3k+2 where k is an integer.
(ii) Show that
(1 - w+w2)(1 - w2 +w4)(1 - w2 +w8) ... to 2n factors = 22n
addikaye03
The A-Team
Alternative Method:Show that
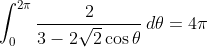
- Rationalise denominator => Partial Fractions.
Haven't checked if it works yet, but i think it would work out alright.
inedible
Member
How about this one,
Prove (1+cos(x) +isin(x))^{n} = (2^{n}cos\frac{x}{2}(cos\frac{nx}{2}+isin\frac{nx}{2}))
P.S. How can I use LaTex?
Prove (1+cos(x) +isin(x))^{n} = (2^{n}cos\frac{x}{2}(cos\frac{nx}{2}+isin\frac{nx}{2}))
P.S. How can I use LaTex?
I think the question is wrong.How about this one,
Prove (1+cos(x) +isin(x))^{n} = (2^{n}cos\frac{x}{2}(cos\frac{nx}{2}+isin\frac{nx}{2}))
P.S. How can I use LaTex?
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
a nice way using eulers:
^n\\=(1+e^{ix})^n\\=\left(e^{i\frac{x}{2}}(e^{-i\frac{x}{2}}+e^{i\frac{x}{2}}) \right )^n\\=(2\cos \frac{x}{2})^n(\cos \frac{x}{2}+i\sin \frac{x}{2})^n\\=2^n\cos^n \frac{x}{2}(\cos \frac{nx}{2}+i \sin \frac{nx}{2}))
Question:
A point P is moving in a circular path around a centre O. Define the angular velocity of P with respect to O at time t.
Derive expressions for the tangential and normal components of the acceleration of P at time t.
A point P is moving in a circular path around a centre O. Define the angular velocity of P with respect to O at time t.
Derive expressions for the tangential and normal components of the acceleration of P at time t.
Aquawhite
Retiring
Aww, I havn't done mechanics yet. I don't think many schools will have :S.Question:
A point P is moving in a circular path around a centre O. Define the angular
velocity of P with respect to O at time t.
Derive expressions for the tangential and normal components of the acceleration of P at time t.
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
Question:
A point P is moving in a circular path around a centre O. Define the angular velocity of P with respect to O at time t.
Derive expressions for the tangential and normal components of the acceleration of P at time t.
amiright?
No.
amiright?
1.
2. It only applies to uniform circular motion.
Let P be at the position at the time t of a point describing a circle of centre O and radius r. OX is a fixed line cutting the circle at A. Suppose that at time t the particle is at P with speed v and at time t+δt it is at Q with speed v+δv.Question:
A point P is moving in a circular path around a centre O. Define the angular velocity of P with respect to O at time t.
Derive expressions for the tangential and normal components of the acceleration of P at time t.
At Q the resolved parts of velocity parallel and perpendicular to OP are (v+δv)sinδθ and (v+δv)cosδθ respectively.
Thus, the resolved parts of increase in velocity during time δt are:
Along tangent at P: (v+δv)cosδθ-v
Along normal at P: (v+δv)sinδθ-0
When δθ is small, sinδθ =:=δθ and using cos2θ=1-2sin2θ
cosδθ=1-2sin2(1/2 δθ) =:= 1 - 2(1/2 δθ)2 =:= 1 (neglecting 2nd order quantities)
Thus, (v+δv)cosδθ-v = δv
and (v+δv)sinδθ-0=vδθ+δvδθ=vδθ (neglecting 2nd order quantities)
Thus, tangential component of accel at P is:
and normal component o accel at P is:
Nice, i was wondering when a 10er would answer this question. btw, it'll never be tested ie Non-uniform circular motion won't ever be tested.Let P be at the position at the time t of a point describing a circle of centre O and radius r. OX is a fixed line cutting the circle at A. Suppose that at time t the particle is at P with speed v and at time t+δt it is at Q with speed v+δv.
At Q the resolved parts of velocity parallel and perpendicular to OP are (v+δv)sinδθ and (v+δv)cosδθ respectively.
Thus, the resolved parts of increase in velocity during time δt are:
Along tangent at P: (v+δv)cosδθ-v
Along normal at P: (v+δv)sinδθ-0
When δθ is small, sinδθ =:=δθ and using cos2θ=1-2sin2θ
cosδθ=1-2sin2(1/2 δθ) =:= 1 - 2(1/2 δθ)2 =:= 1 (neglecting 2nd order quantities)
Thus, (v+δv)cosδθ-v = δv
and (v+δv)sinδθ-0=vδθ+δvδθ=vδθ (neglecting 2nd order quantities)
Thus, tangential component of accel at P is:
and normal component o accel at P is: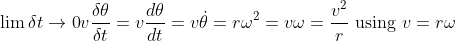
Last edited:
Check the 1981 HSC paper. I think this is from that paper. Oh and I acceleratedNice, i was wondering when a 10er would answer this question. btw, it'll never be tested ie Non-uniform circular motion won't ever be tested.
1981? It may have been but 2010 onwards, they'll never ask it but either way it's very easy to derive. The proofs easier using polar coordinates and a lot quicker.Check the 1981 HSC paper. I think this is from that paper. Oh and I accelerated
Yeah, it's probably not going to be ask anytime soon but it's still in the course. Also, if you check the 1989 HSC paper, they ask for this method (but they don't ask you to derive the tangential component of acceleration), so it's good learning this way too1981? It may have been but 2010 onwards, they'll never ask it but either way it's very easy to derive. The proofs easier using polar coordinates and a lot quicker.
It's a bit like proving DeMovire's theorem using induction. It's never been examined before in the HSC, but it's still examinable...
Last edited:
Gussy Booo
Mathematics <3
the equation:
|z-1-3i|+|z-9-3i|=10 corresponds to an ellipse in the argand diagram
(i) write down the complex number corresponding to the centre
(ii) write down the range of values of arg(z) for complex numbers z, corresponding to points on the ellipse
from hsc past paper =/,
|z-1-3i|+|z-9-3i|=10 corresponds to an ellipse in the argand diagram
(i) write down the complex number corresponding to the centre
(ii) write down the range of values of arg(z) for complex numbers z, corresponding to points on the ellipse
from hsc past paper =/,
