I will assume you don't know how to find stationary points and points of inflexion yet necessary to sketch the curve.
So I will give you a simple effective menu. First note,
If the function has a degree of 1, there will be a smooth line through the intercept.
If the function has an even degree, the curve will bounce off the intercept.
If the function has an odd degree (excluding 1), there will be a little hump on the intercept.
So, factorise first
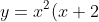(x-2))
So there are zeros (x intercepts) at 0, -2, 2
Now to sketch the curve, since the curve's highest degree is
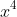
, and the coefficient of it is positive, you start at the top right corner. Place your pencil there. Otherise, if the coefficient of the highest degree is a negative place your pencil at the bottom.
Now, the first intercept,
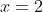
, there is a
degree of 1, so draw a smooth line through it.
Now the second intercept
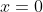
, there is a
degree of 2, the curve will bounce back.
Now the third intercept
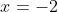
, there is a
degree of 1, so draw a smooth line through it.
You will find the domain is
all real x, and range is
 EDIT
EDIT: Sorry I made a mistake, let me redo question. I don't think it's possible without calculus.
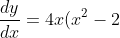)
For stationary points

(x+ \sqrt{2})=0)
Stationary points at
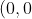)
<- Maximum turning point ,
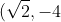)
<- Minimum turning point and
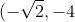)
<- Minimum turning point
