Please help me with this co-ordinate geometry question (: (1 Viewer)

Aysce · Jun 24, 2011

The question is:

Find the distance between the point and the line in each of the following:

(1,4) $3x-4y-12=0$

Thank you in advance to all who take the time in assisting me

it is appreciated greatly!

SpiralFlex · Jun 24, 2011

Use the perpendicular distance formula.

Let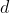 $d$ be our PERPENDICULAR distance.

$d = \left |\frac{ax1+by1+c}{\sqrt{a^2 + b^2}} \right |$

In this case, our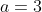 $a = 3$ , $b = -4$ , $c = -12$

Also, $x1 = 1$ , $y1 = 4$

Substitute it in,

$d = \left |\frac{3(1)-4(4)-12}{\sqrt{3^2 + (-4)^2}} \right |$

$\therefore d = 5$ units

Hence our PERPENDICULAR distance from the point $(1,4)$ and the line $3x-4y-12=0$ is $5$ units.

Note: In reality we would not be required to take the absolute value of the denominator as the terms under the square root sign is assumed to be positive. I just put it there for convenience.

Aysce · Jun 24, 2011

Thanks a lot

SpiralFlex · Jun 24, 2011

Aysce said:
Thanks a lot

Feel free to post any more questions up, I have nothing to do for a couple of hours. I am sure others will be able to contribute too.

Aysce · Jun 26, 2011

SpiralFlex said:
Feel free to post any more questions up, I have nothing to do for a couple of hours. I am sure others will be able to contribute too.

Hey spiral !

do you mind helping me with this question?

Find the distance between two lines $2x +y-3=0$ and $2x+y-7=0$

Thanks a million bro

SpiralFlex · Jun 26, 2011

Of course. First, let me point out something. To find the distance between those two curves (perpendicular). You need three things, a point, a line and of course, a pen.

So looking carefully, we only got two lines, no points at all. However we can see that they are parallel. So the perpendicular distance from any point of each graph to the corresponding line will be the same.

Just get a point!

I will take $2x + y - 3 =0$ as my first curve and $2x + y - 7=0$ as my second curve.

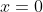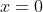On my second curve I will substitute $x = 0$ and get $y = 7$ . Of course we could use any value but $x=0$ is easy!

Now what do we have?

A curve: $2x + y - 3=0$

A point: $(0,7)$

Use perpendicular distance formula now! Let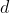 $d$ be the perpendicular distance.

$d= \left |\frac{ax1 + by1+c}{\sqrt{a^2+b^2}} \right |$

Putting our values in,

$d= \left |\frac{2(0) + 1(7)-3}{\sqrt{2^2+1^2}} \right |$

$\therefore d = \frac{4 \sqrt{5}}{5}$ units.

Aysce · Jun 26, 2011

SpiralFlex said:
Of course. First, let me point out something. To find the distance between those two curves (perpendicular). You need three things, a point, a line and of course, a pen.

So looking carefully, we only got two lines, no points at all. However we can see that they are parallel. So the perpendicular distance from any point of each graph to the corresponding line will be the same.

Just get a point!

I will take $2x + y - 3 =0$ as my first curve and $2x + y - 7=0$ as my second curve.

On my second curve I will substitute $x = 0$ and get $y = 7$ . Of course we could use any value but $x=0$ is easy!

Now what do we have?

A curve: $2x + y - 3=0$

A point: $(0,7)$

Use perpendicular distance formula now! Let $d$ be the perpendicular distance.

$d= \left |\frac{ax1 + by1+c}{\sqrt{a^2+b^2}} \right |$

Putting our values in,

$d= \left |\frac{2(0) + 1(7)-3}{\sqrt{4^2+1^2}} \right |$

$\therefore d = \frac{4 \sqrt{17}}{17}$

Err i think the bottom is square root 5, and the answer says its (4 square root of 5) over 5 units :S

SpiralFlex · Jun 26, 2011

Aysce said:
Err i think the bottom is square root 5, and the answer says its (4 square root of 5) over 5 units :S

Correct! Note that SpiralFlex usually makes the most mistake after 9 pm.

powlmao · Jun 27, 2011

SpiralFlex said:
Correct! Note that SpiralFlex usually makes the most mistake after 9 pm.

Which program do you use?

Aysce · Jun 28, 2011

Can anyone answer this question please? It seems pretty simple but perhaps my brain is battered from lack of sleep.. Anyways:

A,B and C are collinear points and AB=BC. If A is the point (4,5) and B is the point (1,-1), find the coordinates of C.

SpiralFlex · Jun 28, 2011

Aysce said:
Can anyone answer this question please? It seems pretty simple but perhaps my brain is battered from lack of sleep.. Anyways:

A,B and C are collinear points and AB=BC. If A is the point (4,5) and B is the point (1,-1), find the coordinates of C.

What does it mean by collinear points? It means that they line on the same straight line. So, how do we answer this question?

Well, we know that AB=BC, so we can say that B is the mid-point of the line.

The mid-point formula:

$M(x,y) = (\frac{x1+x2}{2} , \frac{y1+y2}{2})$

We already know the mid-point! $B (1, -1)$ and we also know one other coordinate $A (4, 5)$

So,

$\frac{4+x2}{2} = 1 , \frac{5+y2}{2}= -1$

$\therefore C (-2, -7)$

j-uhrig said:
Which program do you use?

Click reply then the fx button.

Aysce · Jul 3, 2011

New question! Locus:

Given the points A(1,4) and B(-3,2), find the equation of each locus of the point P(x,y).

c. P is equidistant from A and the x-axis.

Cheers

SpiralFlex · Jul 3, 2011

Aysce said:
New question! Locus:

Given the points A(1,4) and B(-3,2), find the equation of each locus of the point P(x,y).

c. P is equidistant from A and the x-axis.

Cheers

Let's see this question, it may seem tricky, but it very easy to understand.

Now, we have $A (1, 4)$ and $P (x, y)$ .

So what does it mean when $P$ is equidistant from $A$ and the $x$ axis?

It means that the distance of $PA$ will equal to the distance of $P$ to the $x$ axis.

Now let's begin, still remember the distance formula?

$PA = \sqrt{(x-1)^2 + (y-4)^2}$

Now the distance from $P$ to the x axis. We know that $P$ was $(x, y)$ . But what is the point on the $x$ axis? It is $(x, 0)$ . [Since we don't know the $x$ coordinate we must place $x$ in and the $y$ coordinate is always 0 if it lies on the $x$ axis.]

Distance $P$ to $x$ axis = $\sqrt{(x-x)^2 + (y-0)^2}$

$= \sqrt{y^2}$

As for before we said the distances were equal, so:

$\sqrt{(x-1)^2 + (y-4)^2}= \sqrt{y^2}$

Square both sides,

$(x-1)^2 + (y-4)^2 = y^2$

$x^2 - 2x + 1 + y^2 - 8y + 16 = y^2$

$x^2 - 2x + 1 = 8y - 16$

$(x-1)^2 = 8(y-2)$

Oh nice! A parabola! If you have studied the anatomy of a parabola then you would know that the,

Vertex is at $(1,2)$ .

The focal length is $2$ .

Directrix is at $x = 0$ .

The latus rectum is $8$ .

Drongoski · Jul 3, 2011

Very good.

Aysce · Jul 3, 2011

Damn you're good oO thanks

Make a Difference – Donate to Bored of Studies!

Please help me with this co-ordinate geometry question (: (1 Viewer)

Aysce

Well-Known Member

SpiralFlex

Well-Known Member

Aysce

Well-Known Member

SpiralFlex

Well-Known Member

Aysce

Well-Known Member

SpiralFlex

Well-Known Member

Aysce

Well-Known Member

SpiralFlex

Well-Known Member

powlmao

Banned

Aysce

Well-Known Member

SpiralFlex

Well-Known Member

Aysce

Well-Known Member

SpiralFlex

Well-Known Member

Drongoski

Well-Known Member

Aysce

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)