Remember that LIATE is a guide, not a rule. It does not always work.
For example, according to LIATE, Trigonometric functions should be more 'powerful' than algebraic functions ie: sin(x) > x
However, observe the interval
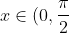)
. The line y=x is clearly dominant over the curve y=sin(x). Furthermore, the tan(x) curve is more dominant over the y=x line within the same interval.
The fact that y=x dominates y=sin(x) can be further verified by observing the limit as x --> infinity of the curve y=sin(x)/x (which oscillates, but slowly converges to 0).
When comparing T with T, or I with I etc, you obviously cannot use LIATE and you may have to resort to a geometrical argument.
You are correct in saying that the tangent function is more 'powerful' than the cosine and sine function. If you had a question involving tan and sin/cos, then the tan function would be the dominating one.
The key thing to remember is what I said earlier...
that LIATE is a guide, not a rule.
