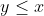Re: 2012 HSC MX2 Marathon
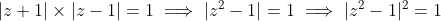
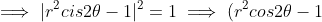^2 +( r^2sin 2\theta)^2 =1)
 -2r^2 cos 2 \theta = 0 \implies r^2 (r^2 - 2cos 2\theta ) = 0 )
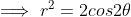
rolpsy's questionYou sure that question's right?
Last edited:
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
rolpsy's questionYou sure that question's right?
Uh thats not the riemann hypothesis...is the riemann hypothesis thing actually syllabus?
Very funny haha.Since we are on important mathematical problems, prove P is not NP.
lol, this is a Riemann sum for an integral. The Riemann hypothesis is a completely different thing altogether.is the riemann hypothesis thing actually syllabus?
Yes lol, I guess my noobness in maths gave it away hahaUh thats not the riemann hypothesis...
Also you're usman, right?
P=NP if P=0 or N=1. So as long as neither of those cases apply, P does not equal NP. Do I get $1,000,000 now?Since we are on important mathematical problems, prove P is not NP.
lol like finding both values of the Heisenberg's Uncertainty Principle!::OSince we are on important mathematical problems, prove P is not NP.
The region ofHere's a nice simple one.
Find the locus of:
Note: Try to use a method that minimises algebra.
How did you come by this answer?The region of