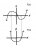To draw a primitive, analyse the original curve, this curve's y-values are the primitive's gradients. If the y-value is high positive, then the gradient of the curve of the primitive is also a high positive value. IF the curve for example, approaches a value of 1 at infinity (asymptote), then the primitive, approaches a gradient of 1 at infinity, so you would get an inclined asymptote, that looks like y=x curve. This came in an exam of ours and had many people stumped. Also, if the value of the original curve is LOW, then the gradient of the primitive, is a negative value as well.
So as a general rule of thumb when sketching primitive functions. Is that when the original curve is:
Above the x-axis ----> The primitive curve is sloping upwards, so its going upwards (increasing y-value).
Below the x-axis -----> The primitive curve is sloping downwards, so its going downwards (decreasing y-value)
At the x-axis ----> Results in the primitive curve having a maximum, minimum or a horizontal point of inflection. **
** Remember, if the curve passes the x-axis from positive to negative, then the primitive is maximum at that point, if it passes through the x-axis going from negative to positive then the primitive is a minimum at that point. If it just touches the x-axis and goes back up again, then its a hor. point of inflection.
Gradient Curve
Its the complete opposite of primitive. Here is the "rule of thumb"
Sloping upwards (increasing y-value) ---> gradient curve is above the x-axis
Sloping Downwards (decreasing y-value) ----> gradient curve is below the x-axis
Stationary Point (gradient = 0 ) ----> gradient curve is an intercept, if its a hor.point of inflection at the original curve, the intercept is the result of the curve "bouncing off" the x-axis
As you can see its the complete opposite, whatever is in bold if you remeber that, you can derive EVERYTHING else. In fact, if you use this definition that I made for simplicity:
"A curve's primitive function's gradient is equal to the value of the original curve at that point, vice versa with the original curve's gradient becoming the gradient curve's y-value"
Using that, you can derive this whole topic.
Edit: If it ever comes up, for some reason, if your original function has a sharp point, then the gradient function is undefined at that point, i.e. it is discontinuous and you should show it by leaving an open circle. Likewise, if there is a discontinuous point in your original function, the primitive will also either have a sharp edge or discontinuous point (best put the latter imo). And if there is a sharp point in your original function the primitive will behave normally based on the values of the original function. But unless your test decides to be REALLY nasty and does that, you probably dont need to worry about this