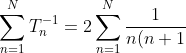}=2\sum_{n=1}^N \frac{1}{n}-\frac{1}{n+1}=2-\frac{2}{N+1}\rightarrow 2\\ \\$as $N\rightarrow \infty)
New number theory questions, ordered roughly by increasing difficulty:
1. Prove that the product of 5 consecutive positive integers cannot be the square of a positive integer.
2. The positive integers m and n satisfy:
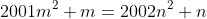
. Prove that m-n is a perfect square.
3. An odd positive integer n is said to be 'sexy' if n divides:
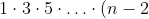+2\cdot 4\cdot 6 \cdot \ldots\cdot (n-1).)
Prove that for any twin prime pair (p,q), EXACTLY one of p,q is sexy.
4. Let a be an arbitrary irrational number. Prove that there are irrational numbers b and b' such that:
-a+b, ab' are both rational,
-a+b', ab are both irrational.

