I have an idea for a proof. Will post when I get home because I will need my trusty tablet

But just for fun, define the set of points bounded by the string and the line to be S such that whatever it doesn't cover is S'.
Then define S to be the outside!
EDIT: Home now
Here is a diagram:
Define a reflective bijection about the given line
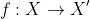
which maps
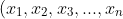 \rightarrow (x_1 ', x_2 ' , ... , x_n '))
as shown below (sorry it looks a bit wonky. Should be an invariant transformation):
So now we have the 'perimeter' of this closed set to be 2L.
By the Isoperimetric Inequality, the area of the region is bounded by:

Where A denotes the area of the closed region. Note that this is a slight variation of the actual inequality since our perimeter is length 2L not L.
But since we want maximal area, we take the supremum:
 = \frac{L^2}{\pi} )
And so this is our maximum area. We now prove that it is in fact a circle.
Suppose we have a circle with circumference length 2L.

But remember that this is the area of
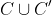
and so since C' is just a (area preserving) bijection of C, we have C = C'
And so therefore our maximum area is:

------------------------------------------------------------------------------
However, I'm not 100% sure how to do this using 4U methods.
My guess would be go construct an arbitrary region (sort of like the use of polar coordinates in evaluating area) and partition it as such:
And sum the areas of the triangles and using Calculus, show that max{A} occurs when the partition lengths are equal in length. Problem is, this doesn't necessarily imply it's a semi-circle...




