goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
This is an easy question (as it's from Math in Focus) but I keep getting the answer wrong.
Could someone please read over my working out and tell me what I did wrong? Thanks
(a) Simplify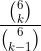
Solution: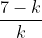 (which is correct according to the answer in the back of the book)
(which is correct according to the answer in the back of the book)
(b) Hence or otherwise, find the greatest coefficient in the expansion of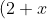^6) .
.
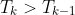
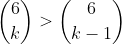
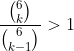
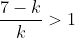
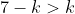
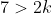
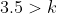
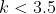
Therefore, for k = 3,2,1, the coefficient of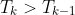
Hence, the term with the greatest coefficient occurs when k = 3
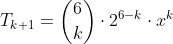
When k = 3,
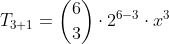
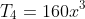
Therefore, greatest coefficient = 160
BUT the answer is actually 240.
Theorem*
Could someone please read over my working out and tell me what I did wrong? Thanks
(a) Simplify
Solution:
(b) Hence or otherwise, find the greatest coefficient in the expansion of
Therefore, for k = 3,2,1, the coefficient of
Hence, the term with the greatest coefficient occurs when k = 3
When k = 3,
Therefore, greatest coefficient = 160
BUT the answer is actually 240.
Theorem*
Last edited:
