Zeta (2) Function (1 Viewer)

[U MAD BRO]

What is the shortest way to prove the function because the one where you use sinx < x < tanx is really really long, elementary but tedious.

Is the proof using Fourier series the shortest one?


and why does = ?!?!?

 

[Carrotsticks]

What is the shortest way to prove the function because the one where you use sinx < x < tanx is really really long, elementary but tedious

Is the proof using Fourier series the shortest one?


and why does = ?!?!?

I would say that the original proof (Euler) using the Taylor Series for the Sine function and equating coefficients is the shortest.

Also, you already have a copy of the proof for that indefinite integral. You use Integration by Parts and the integral reduces to an infinite series, namely zeta_2.

 

[U MAD BRO]

I would say that the original proof (Euler) using the Taylor Series for the Sine function and equating coefficients is the shortest.

Also, you already have a copy of the proof for that indefinite integral. You use Integration by Parts and the integral reduces to an infinite series, namely zeta_2.

Yes, the Euler proof looks both short and simple.

Do you use integration by parts to evaluate that integral? Is the working out simple for that integral?

 

[Carrotsticks]

 

[U MAD BRO]

Thank you a lot

 

[Carrotsticks]

Oh found a little typo, but nothing that will entirely change the proof.

 

[Carrotsticks]

Also in the proof above, I took it for granted that:



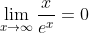
By dominance of functions, but it really should be properly proven (fairly straightforward).

 

[Shadowdude]

Also in the proof above, I took it for granted that:



But the proof is fairly straightforward. Give it a try yourself you're not convinced =)

L'Hopital's rule ftw

 

[U MAD BRO]

Oh found a little typo, but nothing that will entirely change the proof.

Since trials are over, I'll spend my time doing extra curricular stuff, they are so much fun =)

and I used this http://mathim.com/Mathstuff a guy taught me how to do do contour integration there ^_^

 

[Carrotsticks]

Since trials are over, I'll spend my time doing extra curricular stuff, they are so much fun =)

and I used this http://mathim.com/Mathstuff a guy taught me how to do do contour integration there ^_^

It's good to know this extra stuff because it's interesting, but it's probably best if you focus on the HSC for the moment. You have plenty of time for extra reading afterwards.

 

[U MAD BRO]

It's good to know this extra stuff because it's interesting, but it's probably best if you focus on the HSC for the moment. You have plenty of time for extra reading afterwards.

Yes, you're right, but I'll take a break for a week after trials doing extra curricular stuff, and going to the gym, should be a nice break from studying.
Then I'll get back to doing past papers all day =)

 

[math man]

L'Hopital's rule ftw

screw lhopital when you can take adv of taylor

 

[Carrotsticks]

Yep I would have done a proper proof using the Taylor Series too, but I would probably also specify for large x and for all n>0 since x^n can be more powerful than e^x within a fairly large domain, given n is large enough.

 

[Riproot]

^Advertising competitors.

 

[U MAD BRO]

^Advertising competitors.

Stop annoying me or I'll report you.

 

[lolcakes52]

God I love taylor series. When I see a HSC question which uses the first few terms of sin(x) and Newton's method I'm like I SEE WHAT YOU DID THAR!

 

[asianese]

YES! And when it's like e^x < 1+x+x^2/2

But no one at my school has such an appreciation

 

[bleakarcher]

YES! And when it's like e^x < 1+x+x^2/2

But no one at my school has such an appreciation

Don't you mean e^x > 1+x+x^2/2 lol?

 

[U MAD BRO]

Don't you mean e^x > 1+x+x^2/2 lol?

Yeah, it should be.

 

[asianese]

Oh yes, sorry lol

Edit: Actually the question in my trial asked for fx= x-ln(1+x+x^2/2) and it was defined for x<0. It was a calculus inequality with stationary points etc and it ended up being e^x<1+x+x^2/2 for x<0. But for positive x, e^x > 1+x+x^2/2, yes.