HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
BUT I found my domain by drawing the graph
How did you know it was from kπ to (k+1)π
I don't quite understand this part:
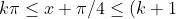\pi )
Please ignore the attachment
I agree!Oops, lol. Hmm..
So the domain is for all x
Using auxilliary angles
So our domain is
?
BUT I found my domain by drawing the graph
How did you know it was from kπ to (k+1)π
I don't quite understand this part:
Please ignore the attachment
Attachments
-
798 bytes Views: 92
Last edited: