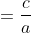When we have a univariate equation of a quadratic we are often to find these roots of the equation, either by factorisation and using null factor law or by the quadratic formula.
For example,

(x-2)=0)

We call 2, 3 the roots (sometimes you hear the word zeros, used interchangeably) of the equation.
We will now define the roots to be alpha and beta. There are only two roots, why? Because this is derived from The Fundamental Theorem of Algebra which is
Every non-zero univariable polynomial with complex coefficients has exactly as many complex roots as its degree.
In simpler terms, a quadratic (degree two) has two complex roots. A cubic has three complex roots. But you don't learn the word "complex roots" until later in your studies. So for now we will agree that some quadratics will have two real roots.
Following the example above,
Let's try
the sum of the roots,

We see we come up with a value of 5. Let's inspect the polynomial,

Doesn't this look like the second term but with a minus sign?
Let's try the
product of the roots,

Let's inspect our polynomial again,

Doesn't this value of 6 agree with the constant term of the polynomial?
Let's see why.
We defined alpha, beta to be the roots of some quadratic equation say,


We can also write it in a products of sums form,
(x-\beta)=0)
If these two expressions are equivalent, we can equate them. So -
(x-\beta))

 x+\alpha \beta)
By equating coefficients of x and the constants,
 =\frac{b}{a})
Sum of the roots:

Or sometimes written as,

Product of the roots,

Or sometimes written as

Alternatively,
Consider the quadratic equation,

We can find the roots by using the quadratic equation formula,


Of course alpha, beta are arbitrarily defined so they can be interchangeable.
Sum of roots,



Product of roots:

Using difference between squares in numerator,
^2-(b^2-4ac)}{4a^2})