HSC 2013 MX2 Marathon (archive) (4 Viewers)

jyu · Nov 28, 2012

Re: HSC 2013 4U Marathon

Trebla said:
Show that for some integer k and constant n:

$\displaystyle\int_0^{\pi}\left(\sin \dfrac{x}{2}\right)^n \cos kx\,dx = \displaystyle\int_0^{\pi}(\sin x)^n \cos 2kx\,dx$

jyu · Nov 29, 2012

Re: HSC 2013 4U Marathon

Carrotsticks said:
Here's a question more accessible to the majority of MX2 students.

$\\ $Suppose $ x + y + z = \frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0$ where $ x,y,z $ are non-zero real numbers.$ \\\\ $Prove that $ \frac{x^6 + y^6 + z^6}{x^3 + y^3 + z^3} = xyz$

x,y,z are non-zero complex numbers?

Carrotsticks · Dec 2, 2012

Re: HSC 2013 4U Marathon

jyu said:
x,y,z are non-zero complex numbers?

I have stated that they are non-zero real numbers.

Sy123 · Dec 2, 2012

Re: HSC 2013 4U Marathon

Carrotsticks said:
I have stated that they are non-zero real numbers.

I just solved it:

http://i981.photobucket.com/albums/ae294/sy08071996/Image4-2.jpg

However I believe that extends it to non-zero complex numbers as well.

Brief explanation of solution:

- Let polynomial have roots x, y, z
Find co-efficients of b, c using 1/x + 1/y + 1/x = x+y+z=0

Leave d alone for now. Sub in x, y, z to create equality with the zero. Then add all 3 equations to get expression for x^3+y^3+z^3
Similarly multiply x^3/y^3/z^3 to each of the 3 previous equations. Find expression for x^6+y^6+z^6

Then simplify and express d=-xyz

cutemouse · Dec 2, 2012

Re: HSC 2013 4U Marathon

Sy123 said:
However I believe that extends it to non-zero complex numbers as well.

Well, there is something called "analytic continuation".

Sy123 · Dec 2, 2012

Re: HSC 2013 4U Marathon

cutemouse said:
Well, there is something called "analytic continuation".

Well yes, if I prove it to be true for complex numbers, then it must be true for the real numbers. But I was just pointing out that the question can be extended to non-zero complex numbers.

jyu · Dec 2, 2012

Re: HSC 2013 4U Marathon

Carrotsticks said:
I have stated that they are non-zero real numbers.

I don't think there are non-zero real numbers x, y and z satisfying x + y + z = 1/x + 1/y + 1/z = 0. If there are such real numbers, what are they?

Rezen · Dec 2, 2012

Re: HSC 2013 4U Marathon

There isn't any. You can prove it by rearranging the conditions to get it in terms of z;

$z = -(x+y) \text{and, } z = \frac{-xy}{x+y}$ .

Then form the difference function $f(x,y) = \frac{-xy}{x+y} +x+y = \frac{x^2+xy+ y^2}{x+y}$

which can be shown with some basic multivariate calculus to not have any zeros among the reals. (well, atleast that's what my quick working shows. I might be wrong.)

Sy123 · Dec 2, 2012

Re: HSC 2013 4U Marathon

Rezen said:
There isn't any. You can prove it by rearranging the conditions to get it in terms of z;

$z = -(x+y) \text{and, } z = \frac{-xy}{x+y}$ .

Then form the difference function $f(x,y) = \frac{-xy}{x+y} +x+y = \frac{x^2+xy+ y^2}{x+y}$

which can be shown with some basic multivariate calculus to not have any zeros among the reals. (well, atleast that's what my quick working shows. I might be wrong.)

Yes I think there are no all three real solutions. This comes from the fact that, if we have a polynomial roots x, y, z with the restrictions in the question.
Then the polynomial equation will be:

$\beta = \alpha^3 + d$

Where it is a polynomial in alpha, and d is any constant, from this equation we can automatically deduce that there can only be 1 real root (and non-zero).

Rezen · Dec 2, 2012

Re: HSC 2013 4U Marathon

Sy123 said:
Yes I think there are no all three real solutions. This comes from the fact that, if we have a polynomial roots x, y, z with the restrictions in the question.
Then the polynomial equation will be:

$\beta = \alpha^3 + d$

Where it is a polynomial in alpha, and d is any constant, from this equation we can automatically deduce that there can only be 1 real root (and non-zero).

That's true. It also gives us that the only possible form of x,y and z are $re^{i\theta},re^{i(\theta+2\pi/3)},re^{i(\theta-2\pi/3)}$ which after a quick substitution prove to be solutions.

cutemouse · Dec 2, 2012

Re: HSC 2013 4U Marathon

Sy123 said:
Well yes, if I prove it to be true for complex numbers, then it must be true for the real numbers.

No actually I THINK it's the other way around... It's been a while since I've done complex analysis though (which is VERY beautiful).

Carrotsticks · Dec 2, 2012

Re: HSC 2013 4U Marathon

cutemouse said:
No actually I THINK it's the other way around... It's been a while since I've done complex analysis though (which is VERY beautiful).

The reals are a subset of C, so if proven true for all C, then it is true for all R. The converse isn't necessarily the same.

RealiseNothing · Dec 2, 2012

Re: HSC 2013 4U Marathon

cutemouse said:
No actually I THINK it's the other way around... It's been a while since I've done complex analysis though (which is VERY beautiful).

The real numbers are apart of the complex numbers though, so proving true for all complex numbers would imply it's true for all real numbers. Like all real numbers can be expressed as a complex number

ie 3 = 3 + 0i

RealiseNothing · Dec 2, 2012

Re: HSC 2013 4U Marathon

Carrotsticks said:
The reals are a subset of C, so if proven true for all C, then it is true for all R. The converse isn't necessarily the same.

or this.

Shadowdude · Dec 2, 2012

Re: HSC 2013 4U Marathon

cutemouse said:
No actually I THINK it's the other way around... It's been a while since I've done complex analysis though (which is VERY beautiful).

you're thinking about analytic continuity, right?

seanieg89 · Dec 3, 2012

Re: HSC 2013 4U Marathon

cutemouse said:
Well, there is something called "analytic continuation".

So? I don't see how that is relevant here.

Shadowdude · Dec 3, 2012

Re: HSC 2013 4U Marathon

I think they just got confused for a bit, personally.

seanieg89 · Dec 4, 2012

Re: HSC 2013 4U Marathon

Straightforward exercise to flex algebra muscles:

Find a polynomial with integer coefficients that has:

$\left(\frac{3}{5}\right)^{1/6}+\left(\frac{5}{3}\right)^{1/6}$

as one of its roots.

Sy123 · Dec 4, 2012

Re: HSC 2013 4U Marathon

DONE:

I'm not bothered to post working out, basically let x = that root, then find x^6, x^4 and x^2 using binomial theorem, then manipulation then:
$6x^6-36x^4+54x^2-245 = 0$

I better not of made a silly mistake :/

==============

$E(x)=\sum_{r=0}^{n} \frac{x^{r}}{r!}$

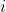$i) Show that E(x) does not have a double root$ \\ \\ $ii) Show that E(x) does not have any real roots if n is even$

seanieg89 · Dec 4, 2012

Re: HSC 2013 4U Marathon

Sy123 said:
DONE:

I'm not bothered to post working out, basically let x = that root, then find x^6, x^4 and x^2 using binomial theorem, then manipulation then:
$6x^6-36x^4+54x^2-245 = 0$

I better not of made a silly mistake :/

==============

$E(x)=\sum_{r=0}^{n} \frac{x^r}{r!}$

$Show that E(x) does not have a double root$

Cbb checking haha but that is the correct idea.

As an addendum to your question, which I think I have asked before:

Prove that E has NO real roots if n is even.

HSC 2013 MX2 Marathon (archive) (4 Viewers)

Member

Member

Retired

This too shall pass

Account Closed

This too shall pass

Member

Member

This too shall pass

Member

Account Closed

Retired

what is that?It is Cowpea

what is that?It is Cowpea

Cult of Personality

Well-Known Member

Cult of Personality

Well-Known Member

This too shall pass

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 4)