Rote learning:
If the discriminant of a quadratic is less than zero, then the polynomial has no real roots.
If equal to zero, exactly one root.
If greater than zero, two distinct roots.
Because the textbook said so.
Not rote learning:
The quadratic formula is
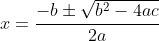
.
But the 'inside' of the square root cannot be negative, otherwise we get complex roots (can't square root a negative number). So if the discriminant is less than zero, there are no real roots.
If it is equal to zero, we simply have
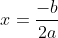
, hence one real root. Notice that it is also the 'formula' for the vertex. This is because we have EXACTLY one root, and this can only occur in a quadratic if it is a double-zero ie: the root IS the vertex.
If greater than zero, we have two DISTINCT roots because of the plus/minus.
===================================
tl;dr rote learners can't explain how it works so don't do it (unless in exceptional circumstances where things MUST be rote learned ie: FTA).
I could go on for ages about the concept of rote learning, but I will save that for a later post.

