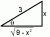METHOD 1 - GENERAL SOLUTION
cosθ(3cosθ - sinθ) = 2sinθcosθ (this is because sin2θ = 2sinθcosθ, a double angle formula for sine)
3cos^2 θ - sinθcosθ - 2sinθcosθ = 0
3cos^2 θ - 3sinθcosθ = 0
3cosθ (cosθ - sinθ) = 0
Solution 1: 3cosθ = 0
cosθ = 0
Now we apply the general solution formula for cosine -
If cosθ = A,
then
 )
In this case, its cosθ = 0, so
 ) θ = +-(pi/2) + n(2pi)
Solution 2:
θ = +-(pi/2) + n(2pi)
Solution 2: sinθ - cosθ = 0
sinθ = cosθ
sinθ/cosθ = 1
tanθ = 1
Now we apply the general solution formula for tan-
If tanθ = A,
then
 )
In this case its tanθ = 1, so
 θ = pi/4 + n(pi)
θ = pi/4 + n(pi)
The 2 general solutions are in red, sub in values of n until u exceed ur domain of θ
I explained the general solutions because the title says it lol
Other methods include: unit circle, or ASTC
METHOD 2 - USE ASTC
1st quadrant: θ (
All sin, cos and tan are positive)
2nd quadrant: (π - θ) (
Sine is positive)
3rd quadrant: (π + θ) (
Tan is positive)
4th quadrant: (2π - θ) (
Cosine is positive)
Solution 1:
cosθ = 0,
Cosine is positive in the 1st and 4th quadrant.
1st quad: Calculate θ
4th quad: Find (2π - θ)
Solution 2:
tanθ = 1,
Tan is positive in the 1st and 3rd quadrant
1st quad: Calculate θ
3rd Quad: Find (θ + π)
-------------------
I tried to explain this to you the best i could because these questions will always appear in the HSC and you must understand how to answer it with CONFIDENCE!