anomalousdecay
Premium Member
- Joined
- Jan 26, 2013
- Messages
- 5,766
- Gender
- Male
- HSC
- 2013
I have posted this thread in light that everyone will benefit from practising these HSC questions.
I tend to have problems with the locus questions of this topic.
To start off:
2005 HSC question 4(c). (5 marks altogether)
The points P(2ap, ap^2) and Q(2aq, aq^2) lie on the parabola x^2 = 4ay.
[The equation of the normal to the parabola at P is x +py = 2ap + ap^3.
The equation of the normal at Q is similarly given by x + qy = 2aq + aq^3.
 Show that the normals at P and Q intersect at the point R whose coordinates are:} )
(-apq(p+q), a( (p^2) + pg + (q^2)+2 )
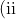 The equation of the chord PQ is y= x(p+q)/2 - apq. (Do not show this).} )
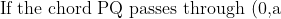, show that pq = -1} )
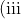 Find the equation of the locus of R if the chord PQ passes through (0,a)} )
I could only get the second part.
I tend to have problems with the locus questions of this topic.
To start off:
2005 HSC question 4(c). (5 marks altogether)
The points P(2ap, ap^2) and Q(2aq, aq^2) lie on the parabola x^2 = 4ay.
[The equation of the normal to the parabola at P is x +py = 2ap + ap^3.
The equation of the normal at Q is similarly given by x + qy = 2aq + aq^3.
(-apq(p+q), a( (p^2) + pg + (q^2)+2 )
I could only get the second part.
Last edited:
