Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
http://www.maths.unsw.edu.au/sites/default/files/final_senior_51.pdf
Problem 1, Scenario 1.
What I was planning to do was, to recursively find the probability of finding people at E on the first night.
So,
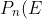 = $Probability that on the$ \ nth \ $night the salesman is at$ \ \ E )
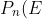 = P_{n-1} (D) )
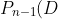 = \frac{1}{2} P_{n-2} (E) + P_{n-2}(C) )
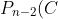 = P_{n-3}(B) = P_{n-4}(A) = \frac{1}{2} P_{n-5} E )
Therefore we arrive at the recurrence relation:
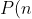 = \frac{1}{2} (P(n-2) + P(n-5)) )
However, I don't know how to find the limiting value of this sequence, making: = L ) doesn't work in this case....
doesn't work in this case....
Any suggestions?
Also, if it comes to the point where evaluating P(1) -> P(5) is necessary, we can just take the cases of if he picks A first, B, C, D, or E first to evaluate the first 5 constants as necessary....
Thanks
Problem 1, Scenario 1.
What I was planning to do was, to recursively find the probability of finding people at E on the first night.
So,
Therefore we arrive at the recurrence relation:
However, I don't know how to find the limiting value of this sequence, making:
Any suggestions?
Also, if it comes to the point where evaluating P(1) -> P(5) is necessary, we can just take the cases of if he picks A first, B, C, D, or E first to evaluate the first 5 constants as necessary....
Thanks
