HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,547
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 2U Marathon
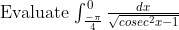
You need to provide more working out when integrating tanx with respect to x
it's funny cos he somehow got the right answer with some errors in the workingYou need to provide more working out when integrating tanx with respect to x
also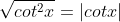
Hm, was this your expression:for part ii) I got \ \ \ \fbox{3} )
i skipped so many steps because i cbfed showing it using this latex bs wastes to much timeYou need to provide more working out when integrating tanx with respect to x
also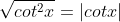
at least in the end of your working, have a quick outline how you integrated tanx with respect to x (unless you memorised it)i skipped so many steps because i cbfed showing it using this latex bs wastes to much time
and mathewYan can you please tell me where i made mistakes?
Lol whoops forgot about the 1/2 at the front of the bracket, (sigh I forgot about trapezoidal rule )Hm, was this your expression:
??
That is what I got initially
Fixed latex, that is the right idea anyway, if you didn't make any mistakes its right
Although your final answer is correct, your working out suggests that the answer is -ln(root2).
