Just some thinking in the shower this morning (I'm a little rusty so forgive me for any errors!).
We have the Riemann-Liouville integral:
 = \frac{1}{\Gamma (q)} \int_{0}^{t} (t - \tau)^{q - 1} f(\tau) d \tau)
So if I take the Laplace transform we get:
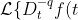 \} = \frac{1}{\Gamma (q)} \mathcal{L} \{ \int_{0}^{t} (t - \tau)^{q - 1} f(\tau) d \tau \})
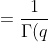} \mathcal{L} \{ t^{q - 1} \} \mathcal{L} \{ f(t) \} \text{ (Convolution)})
}{p^{q}})
I didn't expect that, so it makes me wonder if it's correct? (Then again, after seeing Cauchy weave his magic I shouldn't be too surprised if it is!) Is there a restriction needed on the initial values of the function?
We have the Riemann-Liouville integral:
So if I take the Laplace transform we get:
I didn't expect that, so it makes me wonder if it's correct? (Then again, after seeing Cauchy weave his magic I shouldn't be too surprised if it is!) Is there a restriction needed on the initial values of the function?
