Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2014 MX2 Marathon ADVANCED (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
SilentWaters
Member
- Joined
- Mar 20, 2014
- Messages
- 55
- Gender
- Male
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
+1+1+1+...}{n})
Notice we are adding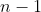 1's to
1's to  (the latter counting for 1 term).
(the latter counting for 1 term).
Sum the components of the product and divide it by the number of terms so that the geometric mean is less than the arithmetic one:Could you explain to me how you get that first line to fit the AM-GM inequality?
Notice we are adding
FrankXie
Active Member
Re: HSC 2014 4U Marathon - Advanced Level
^{\frac1n}=1+\alpha, (1+n)^{\frac1m}=1+\beta, $ so $ \alpha>0, \beta>0 $ and the desired result is $ \frac1{1+\alpha}+\frac1{1+\beta}>1, $ which is equivalent to $ 1+\alpha+1+\beta>(1+\alpha)(1+\beta), $ which is equivalent to $ \alpha\beta<1)
^n=1+n\alpha+$ positive terms $>1+n\alpha, $ so $ m>n\alpha )

well done, so smart! Here is my proof:
by AM-GM. (Noting that not all terms are equal, so we cannot have equality.)
Similarly, we have
Invert these inequalities and sum them to complete the proof.
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
(yes I am guilty of recyling some questions)
Yep that was my method when seanieg89 posted this question near the start of the year
by AM-GM. (Noting that not all terms are equal, so we cannot have equality.)
Similarly, we have
Invert these inequalities and sum them to complete the proof.
(yes I am guilty of recyling some questions)
FrankXie
Active Member
Re: HSC 2014 4U Marathon - Advanced Level
 can be derived neatly by drawing an isosceles triangle with interior anlges being $ 72^\circ, 72^\circ $ and $ 36^\circ. )
}=\frac{2\cos36^\circ}{\frac12-\cos72^\circ}=\frac{\frac{\sqrt5+1}{2}}{\frac12-\frac{\sqrt5-1}{4}}=\frac{2(\sqrt5+1)}{3-\sqrt5} \qquad $ (1)$ )
}=\frac{2\cos108^\circ}{\frac12+\cos36^\circ}=\frac{-\frac{\sqrt5-1}{2}}{\frac12+\frac{\sqrt5+1}{4}}=\frac{-2(\sqrt5-1)}{3+\sqrt5} \qquad $ (2)$ )
Finally adding equations (1) and (2) completes the proof.
Now that you nominated me, i just have my try, not an inspiring method though.perhaps Glitter/ Sy/Frank can tackle the Question (the one I posted)
Finally adding equations (1) and (2) completes the proof.
Last edited:
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
 we make the substitution
we make the substitution  . (This is also motivated by the fact that we are obviously looking for points on the unit circle satisfying a certain condition.)
. (This is also motivated by the fact that we are obviously looking for points on the unit circle satisfying a certain condition.)
Then
^2=1-\cos^2\theta=\sin^2\theta=\cos^2(\pi/2-\theta).)
So/4,\pi(4k-1)/8.)
The 6 distinct solutions are
,\pm\cos(\pi/8),\pm\cos(3\pi/8).)
Since we must have
Then
So
The 6 distinct solutions are
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level

x^{n-1} = x \cdot \frac{d}{dx} \left(\frac{1-x^n}{1-x} \right) )
 \right) \left( \frac{1}{2} \right) - \frac{1}{2} - \frac{1}{2} )

--------------
Please mods keep this thread, just change the title, I'll change my OP
Post any questions within the scope and level of Mathematics Extension 2 mainly targeting Q16 difficulty in the HSC.
Any questions beyond the scope of the HSC syllabus should be posted in the Extracurricular Topics forum:
http://community.boredofstudies.org/238/extracurricular-topics/
Once a question is posted, it needs to be answered before the next question is raised.
I will get the ball rolling:
Prove that
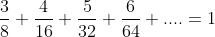
--------------
Please mods keep this thread, just change the title, I'll change my OP
Last edited:
Axio
=o
- Joined
- Mar 20, 2014
- Messages
- 483
- Gender
- Male
- HSC
- 2015
Re: HSC 2014 4U Marathon - Advanced Level
I agree with this.
--------------
Please mods keep this thread, just change the title, I'll change my OP
- Status
- Not open for further replies.
