- Joined
- Feb 16, 2005
- Messages
- 8,477
- Gender
- Male
- HSC
- 2006
Post any questions within the scope and level of Mathematics Extension 2 mainly targeting Q16 difficulty in the HSC.
Any questions beyond the scope of the HSC syllabus should be posted in the Extracurricular Topics forum:
http://community.boredofstudies.org/238/extracurricular-topics/
Once a question is posted, it needs to be answered before the next question is raised.
I encourage all current students in particular to participate in this marathon.
I will get the ball rolling:
Prove that
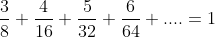
Any questions beyond the scope of the HSC syllabus should be posted in the Extracurricular Topics forum:
http://community.boredofstudies.org/238/extracurricular-topics/
Once a question is posted, it needs to be answered before the next question is raised.
I encourage all current students in particular to participate in this marathon.
I will get the ball rolling:
Prove that
Last edited:
