trantheman
New Member
- Joined
- Feb 21, 2015
- Messages
- 7
- Gender
- Male
- HSC
- 2015
So basically I came across this question and I obtained the part i) (a), but the other two questions/parts I couldn't get. Could anyone help me out here, please???
Volume Shell Method Help. Past HSC Question 1984 (1 Viewer)
- Thread starter trantheman
- Start date
The principle to be used is:
If f(x) is an even function, i.e. f(-x) = f(x), then if you rotate the bum-shaped region about y = b say, then:
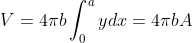
where 'A' is the area of half a bum (part (b) is to show this).
You can now apply this principle to a circle radius 'r Bearing in mind, that the upper semi-circle, radius 'r' and centred at the origin. The upper semi-circle:
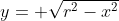
, which is an even function, if we rotate this semi-circle about x=s or x= -s, we get a volume of 
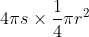
. When you apply same to lower semi-circle you get the same volume. Combining the two, you get the volume of the torus = 
(??)
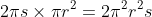
If f(x) is an even function, i.e. f(-x) = f(x), then if you rotate the bum-shaped region about y = b say, then:
You can now apply this principle to a circle radius 'r Bearing in mind, that the upper semi-circle, radius 'r' and centred at the origin. The upper semi-circle:
Last edited:
trantheman
New Member
- Joined
- Feb 21, 2015
- Messages
- 7
- Gender
- Male
- HSC
- 2015
So how is it that you would show part b) and thanks for the reply as well as the help for part c)The principle to be used is:
If f(x) is an even function, i.e. f(-x) = f(x), then if you rotate the bum-shaped region about y = b say, then:
You can now apply this principle to a circle radius 'r Bearing in mind, that the upper semi-circle, radius 'r' and centred at the origin. The upper semi-circle:
?trantheman
New Member
- Joined
- Feb 21, 2015
- Messages
- 7
- Gender
- Male
- HSC
- 2015
Thank you so much for the help. It was much appreciatedConsider 2 vertical strips, one at x = -t and the other at x = t, each of thickness, which will generate a shell of volumes, as shown, when rotated about x = -s.
(s-t) \delta t = 2 \pi f(t)(s-t) \delta t \\ \\ \delta V_2 \backsimeq 2 \pi f(t)(s+t) \delta t \\ \\ \therefore \delta V_1 + \delta V_2 = 2 \pi f(t) (s-t) \delta t + 2 \pi f(t) (s+t) \delta t = 4 \pi s f(t) \delta t \\ \\ \therefore $ total volume $ = \lim _{\delta t \to 0} \sum _ {i} 4 \pi s f(t_i) \delta t = 4 \pi s \int _0 ^r f(t) dt = 4 \pi s A)